《数据结构》第三章栈、队列和数组

Article

数据结构

3.1 栈

3.1.1 栈的基本概念

1. 栈的定义

是只允许在一端进行插入或删除的线性表；LIFO：后进先出。

栈顶（Top）：线性表允许进行插入和删除操作的那一端。
栈底（Bottom）：固定的，不允许进行插入和删除操作的另一端。
空栈：不含任何元素的空表。

2. 栈的基本操作

InitStack(&S)：初始化一个空栈S。
StackEmpty(S)：判空操作。
Push(&S, x)：入栈操作。
Pop(&S, &x)：出栈操作。
GetTop(S, &x)：读取栈顶元素，不出栈。
DestroyStack(&S)：销毁操作。

3.1.2 栈的顺序存储结构

1. 顺序栈的实现

♾️ C 代码:

#define MaxSize 20
typedef struct{
    ElemType data[MaxSize];
    int top;
}SqStack;

栈顶指针：S.top，初始时设置S.top=-1；
栈顶元素：S.data[S.top]。
入栈操作：栈不满时，栈顶指针先加 1，在将值送到栈顶。
出栈操作：栈非空时，先取栈顶元素，再将栈顶指针减 1。
栈空条件：S.top==-1。
栈满条件：S.top==MaxSize - 1。
栈长：S.top + 1。

2. 顺序栈的基本操作

初始化

♾️ C 代码:

void InitStack (SqStack &S){
    S.top = -1;
}

判空操作

♾️ C 代码:

bool StackEmpty (SqStack S){
    if(S.top == -1)    //为空
        return true;
    else            //不空
        return false;
}

入栈操作

♾️ C 代码:

bool Push (SqStack &S, ElemType x){
    if(S.top == MaxSize - 1)
        return false;
    //写法1:
    S.data[++S.top] = x;
    //写法2：
    S.top++;
    S.data[S.top] = x;
}

出栈操作

♾️ C 代码:

bool Pop (SqStack &S, ElemType &x) {
    if(S.top == -1)
        return false;
    //写法1：
    x = S.data[S.top--];
    //写法2：
    x = S.data[S.top];
    S.top--;
}

读取栈顶元素

♾️ C 代码:

bool GetTop (SqStack &S, ElemType &x) {
    if(S.top == -1)
        return false;
    x = S.data[S.top];
    return true;
}

3. 共享栈

利用栈底位置相对不变的特性，让两个顺序栈共享一个一维数组空间，将两个栈的栈底分别设置在共享空间的两端，两个栈顶向共享空间中间延伸。

判空：top0 = -1时 0 号栈为空；top1 = MaxSize时 1号栈为空。
判满：top1 - top0 = 1时，两个指针相邻，即栈满。

共享栈是为了更有效利用存储空间，只有在整个存储空间被占满的时候才发生上溢

3.1.3 栈的链式存储结构

链栈的优点是便于多个栈共享存储空间和提高其效率，且不存在栈满上溢的情况。

通常使用没有头结点的单链表实现链栈，Lhead指向栈顶元素。

♾️ C 代码:

typedef struct LinkNode {
    ElemType data;
    struct LinkNode *next;
}LiStack;

初始化

♾️ C 代码:

void InitLiStack (LiStack &Lhead) {
    Lhead->next = NULL;
    return true;
}

3.2 队列

3.2.1 队列的基本概念

1. 队列的定义

队列是只允许在表的一端进行插入，在表的另一端进行删除；FIFO：先进先出。

队头（Front）：允许删除的一端，也称队首。
队尾（Rear）：允许插入的一端。
空队列：不含任何元素的空表。

2. 队列的基本操作

InitQueue(&Q)：初始化队列。
QueueEmpty(Q)：判空操作。
EnQueue(&Q, x)：入队操作。
DeQueue(&Q, &x)：出队操作。
GetHead(Q, &x)：读取首元素。

3.2.2 队列的顺序存储结构

1. 队列的顺序存储

♾️ C 代码:

#define MaxSize 20
typedef struct {
    ElemType data[MaxSize];
    int front, rear;
}SqQueue;

若队中仅有一个元素，满足rear == MaxSize，但队不满，此时队中出现“上溢出”，这种溢出不是真正的溢出，在data数组中仍然存在可以存放元素的空位置，这是一种假溢出。因此可以使用循环队列解决假溢出问题

2. 循环队列

初始化：Q.front=Q.rear=0。
队首指针进 1：Q.front=(Q.front+1)% MaxSize。
队尾指针进 1：Q.rear=(Q.rear+1)% MaxSize。
队列长度：(Q.rear-Q.front+MaxSize)% MaxSize。
出入队时：指针都按顺时针方向进 1。
区分队空还是队满的情况：
- 牺牲一个单元来区分：入队时少用一个队列单元。
  - 队满：(Q.rear+1)% MaxSize == Q.front 。
  - 队空：Q.front == Q.rear。
  - 队列中元素的个数：(Q.rear-Q.front+MaxSize)% MaxSize。
- 增设size数据成员，表示元素个数。若删除成功，则size-1；若插入成功，则size+1。
  - 队满：Q.size == MaxSize。
  - 队空：Q.size == 0。
- 增设tag数据成员。删除成功，则tag=0；插入成功，则tag=1。
  - 队满：tag == 1 && Q.front == Q.rear。
  - 队空：tag == 0 && Q.front == Q.rear。

3. 循环队列的操作

初始化

♾️ C 代码:

void InitQueue (SqQueue &Q){
    Q.rear = Q.front = 0;
}

判空操作

♾️ C 代码:

bool isEmpty (SqQueue Q) {
    if(Q.rear == Q.front)
        return true;
    else
        return false;
}

入队操作

♾️ C 代码:

bool EnQueue (SqQueue &Q, ElemType x){
    if((Q.rear + 1)% MaxSize == Q.front)
        return false;
    Q.data[Q.rear] = x;
    Q.rear = (Q.rear + 1)% MaxSize;
    return true;
}

出队操作

♾️ C 代码:

bool DeQueue (SqQueue &Q, ElemType &x){
    if(Q.rear == Q.front)
        return false;
    x = Q.data[Q.front];
    Q.front = (Q.front + 1)% MaxSize;
    return true;
}

3.2.3 队列的链式存储结构

1. 队列的链式存储

链式队列一般使用一个同时有队首指针和队尾指针的单链表。

♾️ C 代码:

typedef struct LinkNode{
    ElemType data;
    struct LinkNode *next;
}LinkNode;

typedef struct {
    LinkNode *front,*rear;
}LinkQueue;

不带头结点时，当Q.front == NULL && Q.rear == NULL时，链式队列为空

2. 链式队列的基本操作

初始化

♾️ C 代码:

void InitQueue (LinkQueue &Q){ //带头结点
    Q.front=Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
    Q.front->next = NULL;
}

判空操作

♾️ C 代码:

bool IsEmpty (LinkQueue Q) {
    if(Q.front == Q.rear)
        return true;
    else
        return false;
}

入队操作

♾️ C 代码:

bool EnQueue (LinkQueue &Q, ElemType x) {
    LinkNode *s = (LinkNode*)malloc(sizeof(LinkNode));
    s->data = x;
    s->next = NULL;
    Q.rear->next = s;
    Q.rear = s;
}

出队操作

♾️ C 代码:

bool DeQueue (LinkQueue &Q, ElemType &x) {
    if(Q.front == Q.rear)
        return false;
    LinkNode *p = Q.front->next;
    x = p->data;
    Q.front->next = p->next;
    
    //若原队列中只有一个结点，删除后变空
    if(Q.rear == p)
        Q.rear = Q.front;
    free(p);
    return true;        
}

3.2.4 双端队列

理解即可

通常考察以下两种受限的双端队列：

输出受限的双端队列
允许在一端进行插入和删除，另一端只允许插入。
输入受限的双端队列
允许在一端进行插入和删除，另一端只允许输出。

3.3 栈和队列的应用

3.3.1 栈在括号匹配中的应用

算法的思想如下
- 初始设置一个空栈，顺序读入括号。
- 若是左括号，则压入栈中。
- 若是右括号，则将栈中栈顶的左括号弹出，进行匹配。
匹配失败的情况
- 左括号单身：右括号匹配完后，栈中还有左括号。
- 右括号单身：右括号进行匹配时，栈中没有左括号。
- 左右不匹配：右括号和左括号进行匹配时，发现形式不同。如：[ 和 )。

代码实现

♾️ C 代码:

#define MaxSize 100

// 栈的定义
typedef struct {                
    char data[MaxSize];
    int top;
}Stack;

// 初始化
void initStack (Stack *s){        
    s->top = -1;
}

// 检查栈是否为空
bool isEmpty(Stack *s) {        
    return s->top == -1;
}

// 入栈操作
bool push(Stack *s, char c) {    
    if (s->top >= MaxSize - 1) {
        return false; // 栈满
    }
    s->data[++s->top] = c;
    return true;
}

// 出栈操作
bool pop(Stack *s, char *x) {    
    if (isEmpty(s)) {
        return false;
    }
    x = s->data[s->top--]
    return true;
}

// 检查括号是否匹配
bool isValid(char *str) {        
    Stack stack;
    initStack(&stack);

    for (int i = 0; str[i] != '\0'; i++) {
        char c = str[i];
        if (c == '(' || c == '[' || c == '{') {
            push(&stack, c);
        } else if (c == ')' || c == ']' || c == '}') {
            if (isEmpty(&stack)) {
                return false; // 栈为空但遇到右括号(右括号单身)
            }
            char *top;
            pop(&stack, top);
            // 检查括号是否匹配（左右不匹配）
            if ((c == ')' && top != '(') || 
                (c == ']' && top != '[') || 
                (c == '}' && top != '{')) {
                return false;
            }
        }
    }
    return isEmpty(&stack); // 最后检查栈是否为空（左括号单身）
}

3.3.2 栈在表达式求值中的应用

1. 算术表达式

中缀表达式：人们常用的算术表达式。如：(3+4)*5/2。
前缀表达式：又称波兰表达式。如：/*+3452。
后缀表达式：又称逆波兰表达式。如：34+5*2/。

2. 中缀表达式转后缀表达式

左优先原则，同理，中转前使用右优先原则

遇到操作数。直接加入后缀表达式。
遇到界限符。
- 若为 (，则直接入栈。
- 若为 )，则不入栈，且依次弹出栈中的运算符并加入后缀表达式，直到遇到(为止，并直接删除(。
遇到运算符。
- 若其优先级高于栈顶运算符或遇到栈顶为(，则直接入栈。
- 若其优先级低于或等于栈顶运算符，则依次弹出栈中的运算符并加入后缀表达式，直到遇到一个优先级低于它的运算符或遇到 (或栈空为止，之后将当前运算符入栈。

3. 后缀表达式求值

过程：从左往右依次扫描后缀表达式的每一项：
- 若是操作数，则将其压入栈中。
- 若是操作符<OP>，则从栈中弹出两个操作数Y和X，形成运算指令X<OP>Y，并将计算结果压入栈中。
  特别注意：操作数Y和X最后的运算指令顺序；若操作符是-和/，操作数的顺序及其重要！！

代码实现：

♾️ C 代码:

double* evaluatePostfix(char *postfix) {
    Stack stack;
    initStack(&stack);  // 初始化操作数栈

    int i = 0;
    while (postfix[i] != '\0') {
        // 跳过空格
        if (postfix[i] == ' ') {
            i++;
            continue;
        }

        // 处理数字（包括多位数）
        if (isdigit(postfix[i])) {
            double num = 0;
            // 将连续的数字字符转换为整数
            while (isdigit(postfix[i])) {
                num = num * 10 + (postfix[i] - '0');
                i++;
            }
            push(&stack, num);  // 将数字压入栈
        }
        // 处理运算符
        else {
            // 弹出两个操作数（注意顺序）
            double *a,*b;
            pop(&stack, b)
            pop(&stack, a);
            
            // 根据运算符进行计算
            switch (postfix[i]) {
                case '+':
                    push(&stack, a + b);
                    break;
                case '-':
                    push(&stack, a - b);
                    break;
                case '*':
                    push(&stack, a * b);
                    break;
                case '/':
                    if (b == 0) {
                        printf("错误：除数不能为零\n");
                        exit(EXIT_FAILURE);
                    }
                    push(&stack, a / b);  // 使用浮点除法
                    break;
                default:
                    printf("无效运算符：%c\n", postfix[i]);
                    exit(EXIT_FAILURE);
            }
            i++;  // 移动到下一个字符
        }
    }

    // 最终栈中应只剩一个元素
    if (stack.top != 0) {
        printf("无效的后缀表达式\n");
        exit(EXIT_FAILURE);
    }
    
    double *result;
    pop(&stack, result)
    return result;  // 返回最终结果
}

3.3.3 栈在递归中的应用

递归是一种重要的程序设计方法。
递归模型不能是循环定义的，必须满足两个条件：
- 递归表达式（递归体）。
- 边界条件（递归出口）。
递归算法转换为非递归算法，通常需要借助栈来实现这种转换。

递归调用过程中，系统会存储每一层的返回点、局部变量、传入实参。所以递归次数过多容易造成栈溢出。同时效率不高的原因是调用过程中包含很多重复的计算

3.3.4 队列在层次遍历中的应用

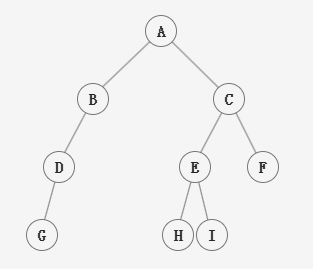
序号	说明	队内	队外
1	A入	A
2	A出，BC入	BC	A
3	B出，D入	CD	AB
4	C出，EF入	DEF	ABC
5	D出，G入	EFG	ABCD
6	E出，HI入	FGHI	ABCDE
7	F出	GHI	ABCDEF
8	GHI出		ABCDEFGHI

过程：

1. 根结点入队。
1. 若队空，则结束遍历；否则重复3 操作。
1. 队列中第一个结点出队。若其有左孩子，则将左孩子入队；若有右孩子，则将右孩子入队，返回 2操作。

3.3.5 队列在计算机系统中的应用

解决主机与外部设备之间速度不匹配的问题。（缓冲区，如：打印机）
解决由多用户引起的资源竞争问题。（CPU资源竞争）

3.4 数组和特殊矩阵

3.4.1 数组的定义

每个数据元素称为一个数组元素。
每个元素在$n$个线性关系中的序号称为该元素的下标。
数组与线性表关系：数组是线性表的推广。
- 一维数组可视为一个线性表。
- 二维数组可视为是定长数组的线性表。

3.4.2 数组的存储结构

一维数组A[0...n-1]，其存储结构关系式：
$$ LOC(a_i)=LOC(a_0)+i\times L (0\le i<n) $$
$L$是每个数组元素所占的存储单元。
二维数组：$i$：行标；$j$：列标
- 行优先存储
  $$ LOC(a_{i,j} )=LOC(a_{0,0} )+(i\times 行数+j)\times L $$

列优先存储
$$ LOC(a_{i,j} )=LOC(a_{0,0} )+(j\times 行数+i)\times L $$

3.4.3 特殊矩阵的压缩存储

1. 对称矩阵

元素$a_{i,j}$在数组 B 中的下标 $k=1+2+……+(i-1)+j-1=\frac{i(i-1)}{2}+j-1$ （数组B 下标从 0 开始）

存储下三角区和主对角线元素
$$ k= \begin{cases} \frac{i(i-1)}{2}+j-1\hspace{5mm}& i\ge j(存储下三角区和主对角线元素)\\ \frac{j(j-1)}{2}+i-1 & i<j(上三角区元素) \end{cases} $$
存储上三角区和主对角线元素
$$ k= \begin{cases} \frac{(i-1)(2n-i+2)}{2}+(j-i)\hspace{5mm}& i\ge j(存储上三角区和主对角线元素)\\ \frac{(j-1)(2n-j+2)}{2}+(i-j) & i<j(下三角区元素) \end{cases} $$

2. 三角矩阵

存储下三角区和主对角线元素
$$ k= \begin{cases} \frac{i(i-1)}{2}+j-1\hspace{5mm}& i\ge j(存储下三角区和主对角线元素)\\ \frac{n(n+1)}{2} & i<j(上三角区元素) \end{cases} $$
存储上三角区和主对角线元素
$$ k= \begin{cases} \frac{(i-1)(2n-i+2)}{2}+(j-i)\hspace{5mm}& i\ge j(存储上三角区和主对角线元素)\\ \frac{n(n+1)}{2} & i<j(下三角区元素) \end{cases} $$

3. 三对角矩阵

按行优先原则，$a_{i,j}$是第几个元素？

前 $i-1$ 行：共 $3(i-1)-1$ 个元素
$a_{i,j}$在第 $i$ 行的第 $j-i+2$ 个元素
$a_{i,j}$是第 $2i+j-2$ 个元素

3.4.4 稀疏矩阵

三元组（行标$i$，列标$j$，值$a_{i,j}$）
十字链表存储（见第六章第二节）

现在已有 122 次阅读，0 条评论，1 人点赞

日	一	二	三	四	五	六
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

《数据结构》第三章 栈、队列和数组

3.1 栈

3.1.1 栈的基本概念

1. 栈的定义

2. 栈的基本操作

3.1.2 栈的顺序存储结构

1. 顺序栈的实现

2. 顺序栈的基本操作

3. 共享栈

3.1.3 栈的链式存储结构

3.2 队列

3.2.1 队列的基本概念

1. 队列的定义

2. 队列的基本操作

3.2.2 队列的顺序存储结构

1. 队列的顺序存储

2. 循环队列

3. 循环队列的操作

3.2.3 队列的链式存储结构

1. 队列的链式存储

2. 链式队列的基本操作

3.2.4 双端队列

3.3 栈和队列的应用

3.3.1 栈在括号匹配中的应用

3.3.2 栈在表达式求值中的应用

1. 算术表达式

2. 中缀表达式转后缀表达式

3. 后缀表达式求值

3.3.3 栈在递归中的应用

3.3.4 队列在层次遍历中的应用

3.3.5 队列在计算机系统中的应用

3.4 数组和特殊矩阵

3.4.1 数组的定义

3.4.2 数组的存储结构

3.4.3 特殊矩阵的压缩存储

1. 对称矩阵

2. 三角矩阵

3. 三对角矩阵

3.4.4 稀疏矩阵

《数据结构》第三章栈、队列和数组