2.1 数制与编码
2.1.1 进位计数制及其相互转换
1. 进位计数制
- 基数:每个数位所用到不同数码的个数(r 进制的基数是 r)
- 位权($K_n$)
一个 r 进制数的数值表示为:
$K_{n}r^{n}+K_{n-1}r^{n-1}+……+K_{0}r^{0}+K_{-1}r^{-1}+……+K_{-m}r^{-m}$
- 十进制:D
- 二进制:B
- 八进制:O
- 十六进制:H 或者前缀0x
2. 不同进制数的相互转换
- 二<->八或十六

八->十六:八->二->十六
十六->八:十六->二->八 - 任意->十
讲任意制数的各位数码($r^n$)与它们的权值($K_n$)相乘,再相加 十->任意
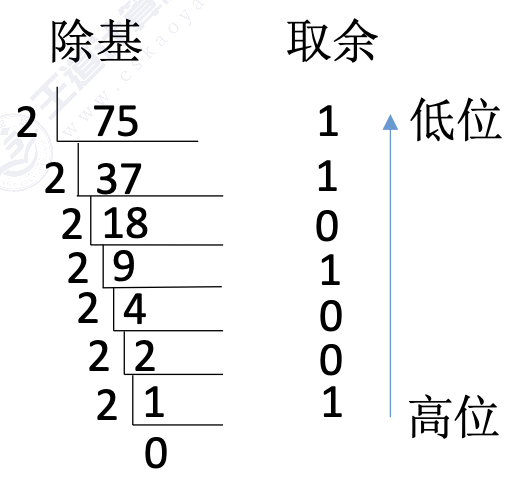
- 整数部分:除基取余法

- 小数部分:乘基取整法

2.1.2 定点数的编码表示
1. 真值和机器数
真值:符合人类习惯的,带“+”或“-”符号的数
机器数:将符号“数字化”,用“0”表示“正”,用“1”表示“负”的数- 整数部分:除基取余法
2. 机器数的定点表示
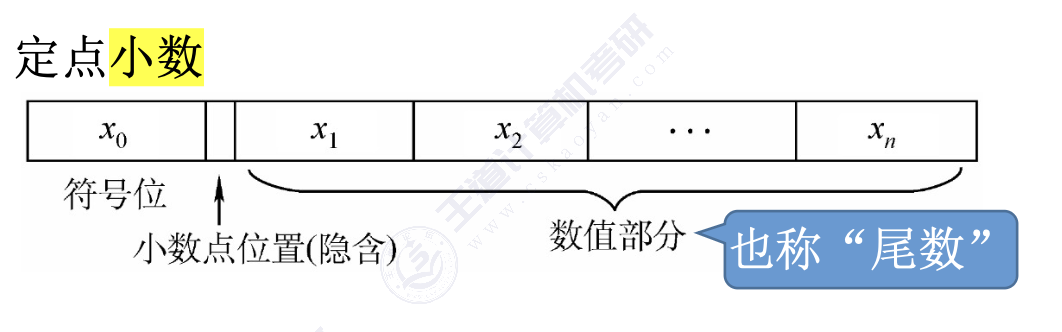
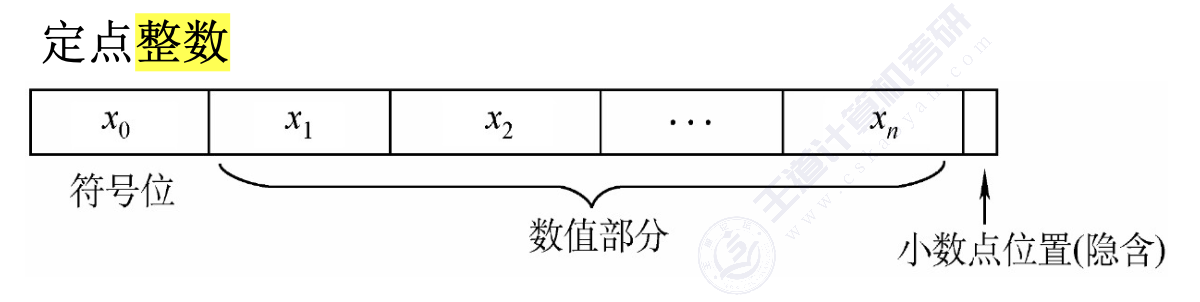
定点数:小数点的位置固定(常规计数)
- 定点小数:纯小数

- 定点整数:纯整数

- 定点小数:纯小数
- 浮点数:小数点的位置不固定(科学计数)
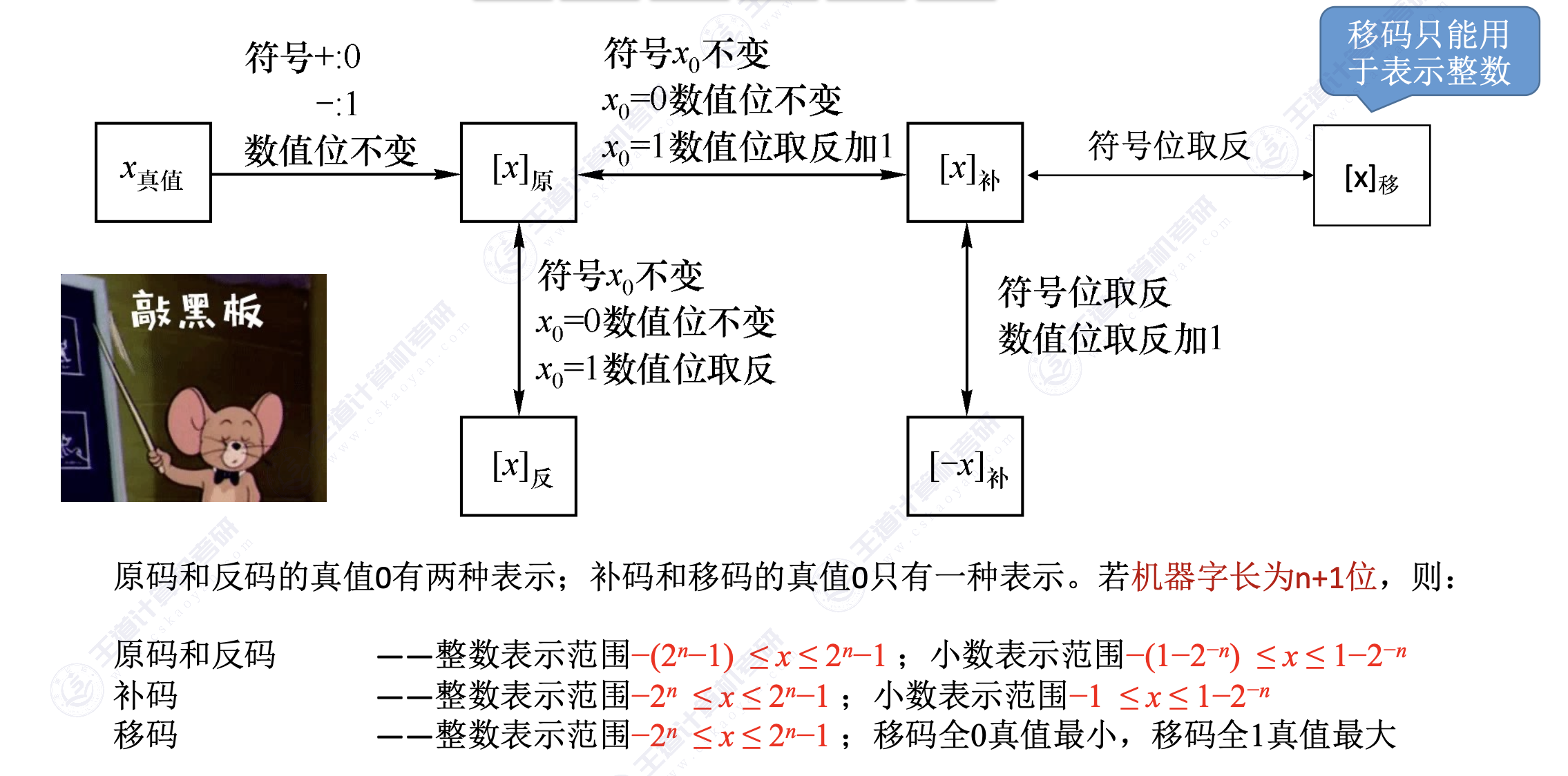
3. 原码、反码、补码、移码
原码
- 用机器数的最高位表示数的符号,其余各位表示数的绝对值。
- 若字长为 n+1,则原码整数的表示范围为:$-(2^n-1)\le x\le 2^n-1$(关于原点对称)
零的原码表示有正零和负零两种形式
- [+0]=0,0000000
- [-0]=1,0000000
优点
- 与真值对应关系简单、直观,与真值转换简单
- 用原码实现乘除运算比较简便
缺点
- 0的表示不唯一
- 用原码实现加减运算比较复杂
反码
- 在计算机内部,反码是原码转换补码的中间表示形式
- 负数的反码可采用“按位取反”
- 正数的反码和原码相同
- 若字长为 n+1,则反码整数的表示范围为:$-(2^n-1)\le x\le 2^n-1$(关于原点对称)
零的反码表示有正零和负零两种形式
- [+0]=0,0000000
- [-0]=1,1111111
缺点
- 0的表示不唯一
- 表示范围比补码少一个最小负数
补码
- 加减运算统一采用加法操作实现
- 正数的补码=其原码
- 负数的补码=其原码数值位取反+1=反码末位+1
- 若字长为 n+1,则补码整数的表示范围为:$-2^n\le x\le 2^n-1$,小数部分:$-1\le x\le 1-2^{-n}$
零的补码只有一种表示方式
- [+0]=[-0]=0,0000000
- 已知[x]的补码,[-x]的补码=[x]所有位取反,末位加一
移码
- 表示浮点数的阶码
- 只能表示整数
- 移码=真值+一个偏置值=补码符号位取反
零的移码只有一种表示方式
- [+0]=[-0]=1,0000000
- 移码保持了数据原有的大小顺序,移码大真值就大,移码小真值就小
4. 原、反、补、移码总结
2.1.3 整数的表示
1. 无符号整数
一个编码的全部二进制位均为数值位,而没有符号位
2. 有符号整数
将符号数值化,将符号位放在有效数字的前面
2.1.4 C语言中的整数类型及类型转换
1. C语言中的整型数据类型
无符号关键字:unsigned
短整型(2字节,16bit位):short int
整型(四字节,32bit位):int
长整型(32位机:四字节,32bit位;64位机:八字节,64bit位):long int
上述类型均以 补码形式 存储。
2. 有符号数和无符号数的转换
有符号->无符号
♾️ C 代码:int main(){ short x = -4321; unsigned short y = (unsigned short) x; printf("x = %d, y = %u",x,y); }输出:
♾️ C 代码:x = -4321, y = 61215$[x]_原=1,001000011100001,[x]_补=1,110111100011111$
$[y]_原=[y]_补=1110111100011111=61215D$无符号->有符号
♾️ C 代码:int main{ unsigned short x = 65535; short y = (short) x; printf("x = %u, y = %d",x,y); }输出:
♾️ C 代码:x = 65535, y = -1$[x]_原=[x]_补=1111111111111111$
$[y]_补=1,111111111111111,[y]_原=1,000000000000001=-1D$
3. 不同字长整数之间的转换
大字节->小字节
♾️ C 代码:int main(){ int x = 165537, u = -34991; short y = (short) x, v = (short) u; printf("x = %d, y = %d\n",x,y); printf("u = %d, v = %d",u,v); }输出:
♾️ C 代码:x = 165537, y = -31071 u = -34991, v = 30545大字节变小字节:高位截断,保留低位
$[x]_原=[x]_补=0,0000000000000101000011010100001=000286A1 H$
$[y]_补=1,000011010100001,[y]_原=1,111100101011111=-31071 D$
$[u]_原=[u]_补=1,0000000000000001000100010101111=800088AF H$
$[v]_补=1,000100010101111,[v]_原=1,111011101010001=-30545 D$
小字节->大字节
♾️ C 代码:int main(){ short x = -4321; int y = x; unsigned short u = (unsigned short) x; unsigned int v = u; printf("x = %d, y = %d\n",x,y); printf("u = %u, v = %u",u,v); }输出:
♾️ C 代码:x = -4321, y = -4321 u = 61215, v = 61215小字节变大字节:高位补符号位(负补 1,正补 0)
$[x]_原=1,001000011100001,[x]_补=1,110111100011111$
$[y]_补=1,1111111111111111110111100011111$
$[y]_原=1,00000000000001000011100001=-4321 D$
$[u]_补=1110111100011111=[u]_原=61215D$
$[v]_原=[v]_补=00000000000000001110111100011111=61215D$
2.2 运算方法和运算电路
2.2.1 基本运算部件
运算器由算术逻辑单元(ALU)、移位器、状态寄存器(PSW)、通用寄存器等组成。其中 ALU 核心部件是加法器。
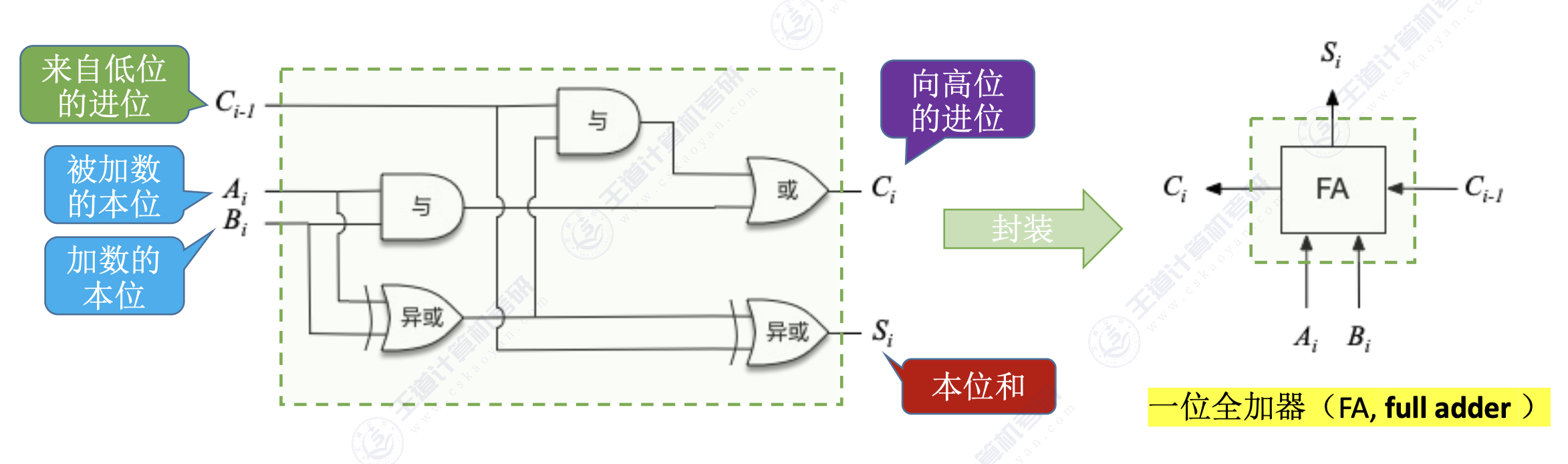
1. 一位全加器
设 $A_i$ 为被加数的本位,$B_i$ 为加数的本位,$C_{i-1}$ 为来自低位的进位,$S_i$ 为本位和
- 本位和 $S_i=A_i\oplus B_i\oplus C_{i-1}$ (当三者之中有奇数个 1 时,本位和为 1 ,否则为 0 )
- 当前高位的进位 $C_{i}=A_iB_i+(A_i\oplus B_i)C_{i-1}$ (当AB都为1时;或者AB两者有一个 1,且低位为1时,高位的进位为 1,否则为 0 )

2. 串行进位加法器
将 n 个全加器相连,即可得到 n 位加法器,称为串行进位加法器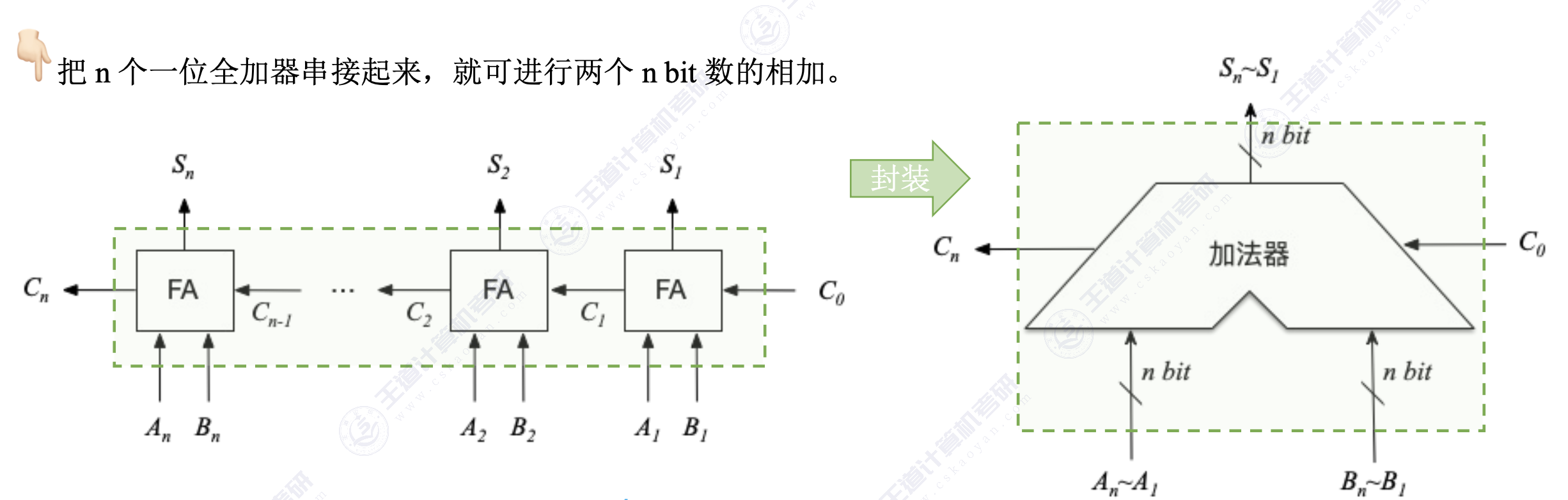
不足之处
- 进位信息是串行连接的,计算速度取决于进位信息产生和传递速度
- 位数越多,运算速度越慢
3. *并行进位加法器
也称先行进位加法器:将 n 个一位全加器连接上 n 位的先行进位部分(简称 CLA部件),使其“并行产生进位”,从而加快运算速度。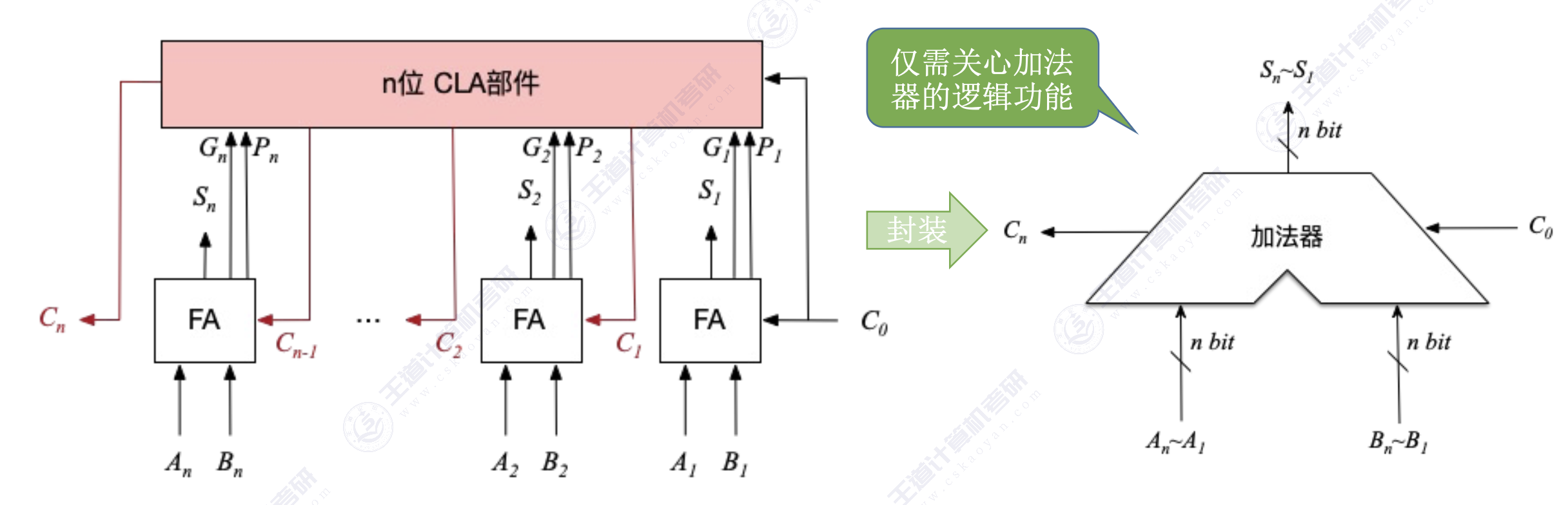
不足之处
- 随着加法器位数的增加,电路结构会变得更复杂。
4. 带标志加法器
主要作用:关注加法运算是否发生溢出、运算结构的正负性、运算结果是否为 0等。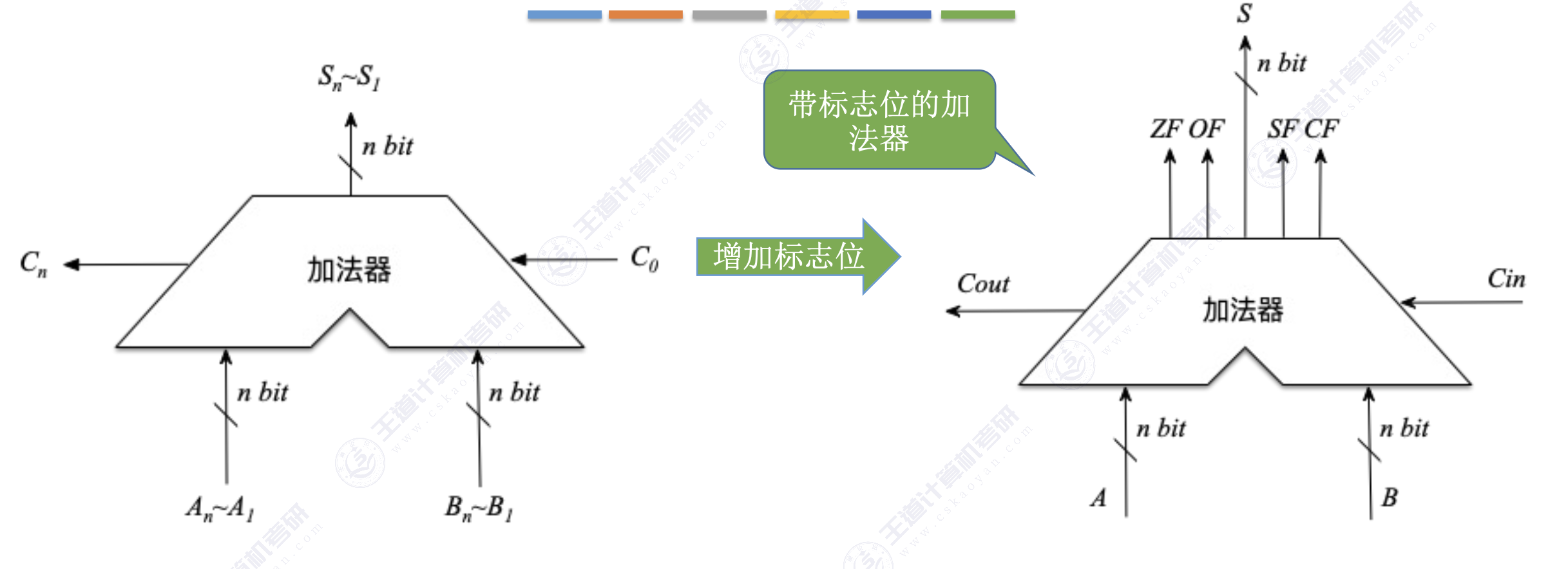
溢出标志 OF
- 判断有符号数的加减运算是否溢出
- $OF=C_n\oplus C_{n-1}$
- $OF=0$ 表示未溢出
- $OF=1$ 表示溢出
符号标志 SF
- 表示有符号数的加减运算结果的正负性
- $SF=F_{n-1}$
- $SF=0$ 表示为正数
- $SF=1$ 表示为负数
零标志 ZF
- 用于判断加减运算的结果是否为0
- $ZF=0$ 表示结果不为0
- $ZF=1$ 表示结果为0
进位/借位标志 CF
- 判断无符号数的加减运算是否溢出
- $CF=C_{out}\oplus C_{in}$
- $CF=0$ 表示未溢出
- $CF=1$ 表示溢出
5. 算术逻辑单元
ALU 是一种功能较强的组合逻辑电路,能进行多种算术运算和逻辑运算。
- 若ALU 支持 k 种功能,则控制信号(ALUop)的位数为 $\left \lceil \log_{2}{k} \right \rceil$
- ALU 的运算数、运算结果位数与计算机机器字长相同
- ALU 也可以实现左移或者右移的移位操作
2.2.2 定点数的移位运算
移位:通过改变各个数码位和小数点的相对位置
1. 逻辑移位
- 常用处理无符号整数
左移:高位移除,低位补 0
- 若高位移除后,符号位前后不一样,则发生溢出
右移:低位移除,高位补 0
- 若低位移除的是 1,则会丢失精度
2. 算术移位
- 常用处理有符号整数
左移:高位移除,低位补 0
- 若高位移除的是 1,则发生溢出
右移:低位移除,高位补 符号位
- 若低位移除的是 1,则会丢失精度
2.2.3 定点数的加减运算
1. 补码的加减运算
设机器字长为 $n+1$
加法
- $[A+B]_补=[A]_补+[B]_补 (mod 2^{n+1})$
减法
- $[A-B]_补=[A]_补+[-B]_补(mod 2^{n+1})$
- 其中$[-B]_补=[B]_补 包括符号位全部取反,末位加 1$
2. 溢出判别方法
仅当两个符号相同的数相加或两个符号相异的数相减才可能产生溢出。
- 上溢:正+正->负
- 下溢:负+负->正
判断溢出的方法
- 采用一位符号位(模2补码)
$设A的符号为A_s,B的符号为B_s,运算结果的符号为S_s$
$V=A_sB_S \overline{S_s}+\overline{A_s} \overline{B_s}S_s$
$V=0:表示无溢出;V=1:表示有溢出$ - 采用双符号位(模4补码)
$双符号位S_{s1}、S_{s2}$
$V = S_{s1}\oplus S_{s2}$
$V=0:表示无溢出;V=1:表示有溢出$
$①S_{s1}S_{s2}==00:表示结果为正数,无溢出$
$②S_{s1}S_{s2}==01:表示结果正溢出$
$③S_{s1}S_{s2}==10:表示结果负溢出$
$④S_{s1}S_{s2}==11:表示结果为负数,无溢出$ - 采用一位符号位根据数值位的进位情况判断(溢出标志 OF)
见 2.2.1-4
- 采用一位符号位(模2补码)
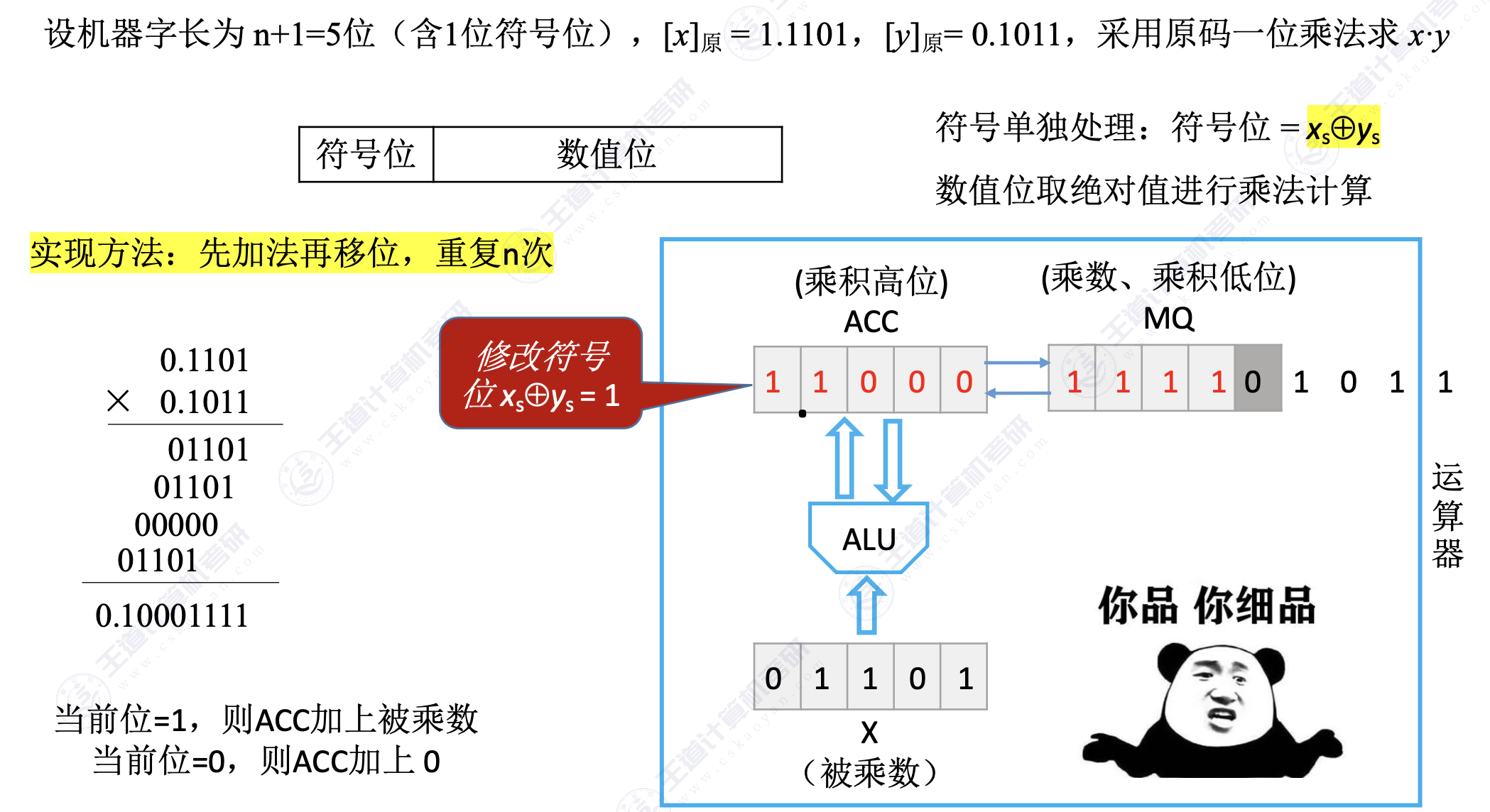
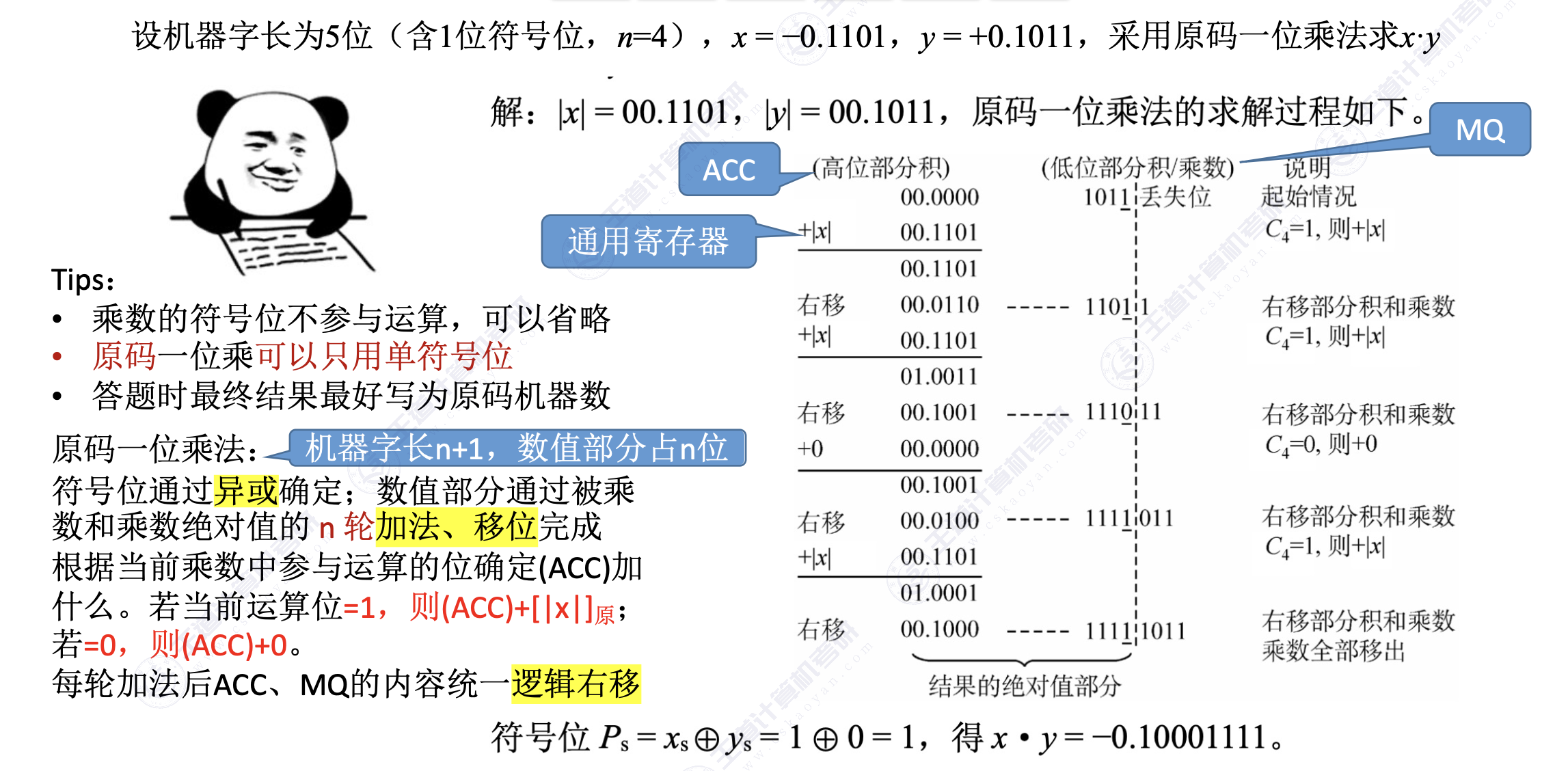
2.2.4 定点数的乘除运算
1. 乘法运算
- 逻辑右移
- 乘数的符号位不参与运算


2. 除法运算
逻辑左移
符号位参与运算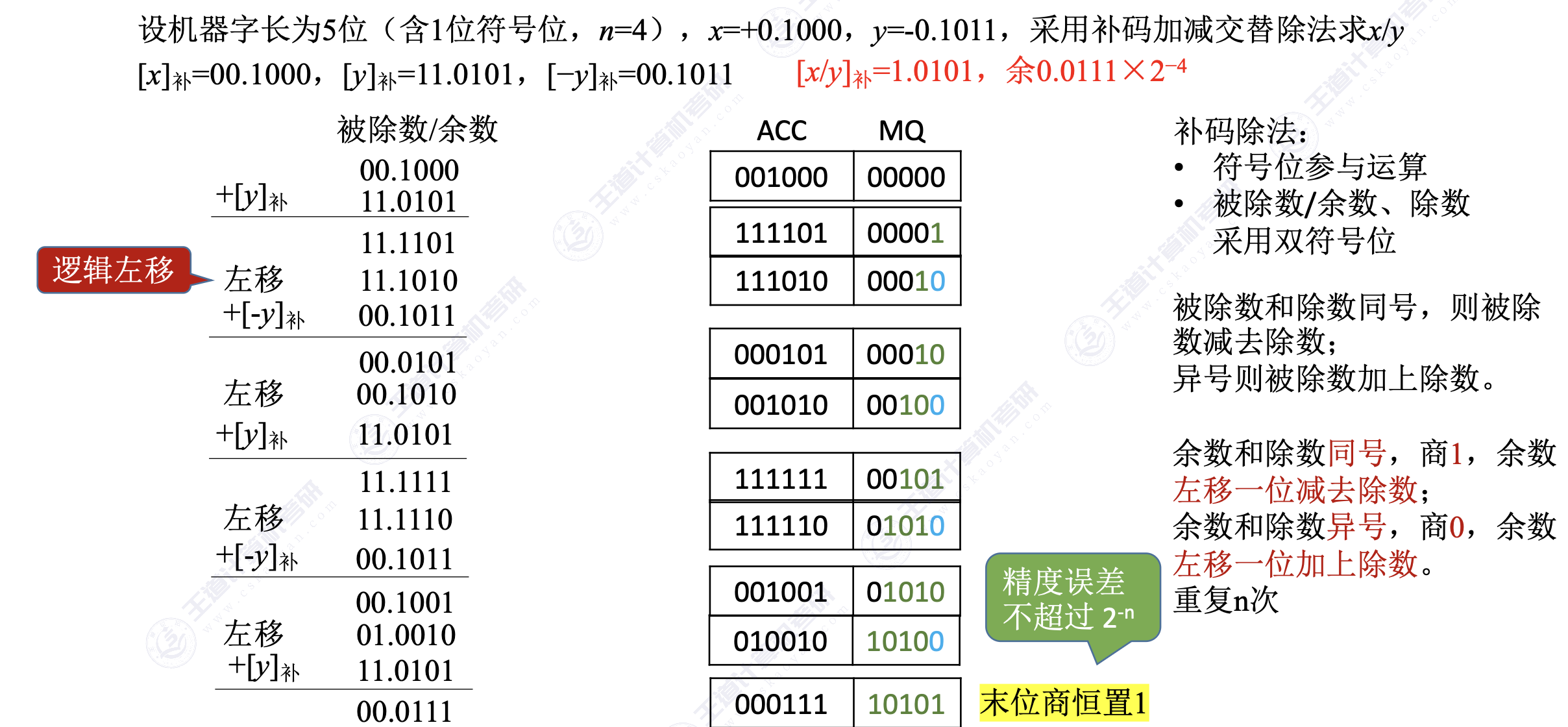
2.3 浮点数的表示与运算
2.3.1 浮点数的表示
1. 浮点数的表示格式
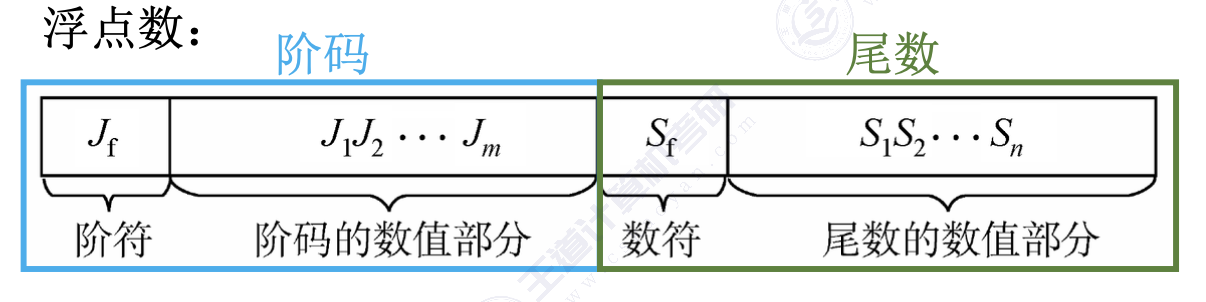
- 阶码:常用补码或移码表示的定点整数
- 尾数:常用原码或补码表示的定点小数
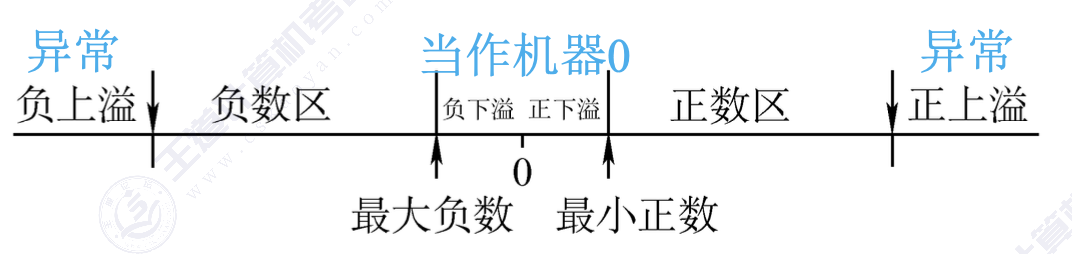
2. 浮点数的表示范围
3. 浮点数的规格化
规格化操作:尽可能多地保留有效数字的位数,使有效数字尽量占满尾数数位
左归
- 通过算术左移,阶码减一的方式 进行规格化
- 左归可能要进行多次
右归
- 通过算术右移,阶码加一的方式 进行规格化
- 右归时,阶码增加可能导致溢出
- 规格化的特点

4. IEEE 754标准
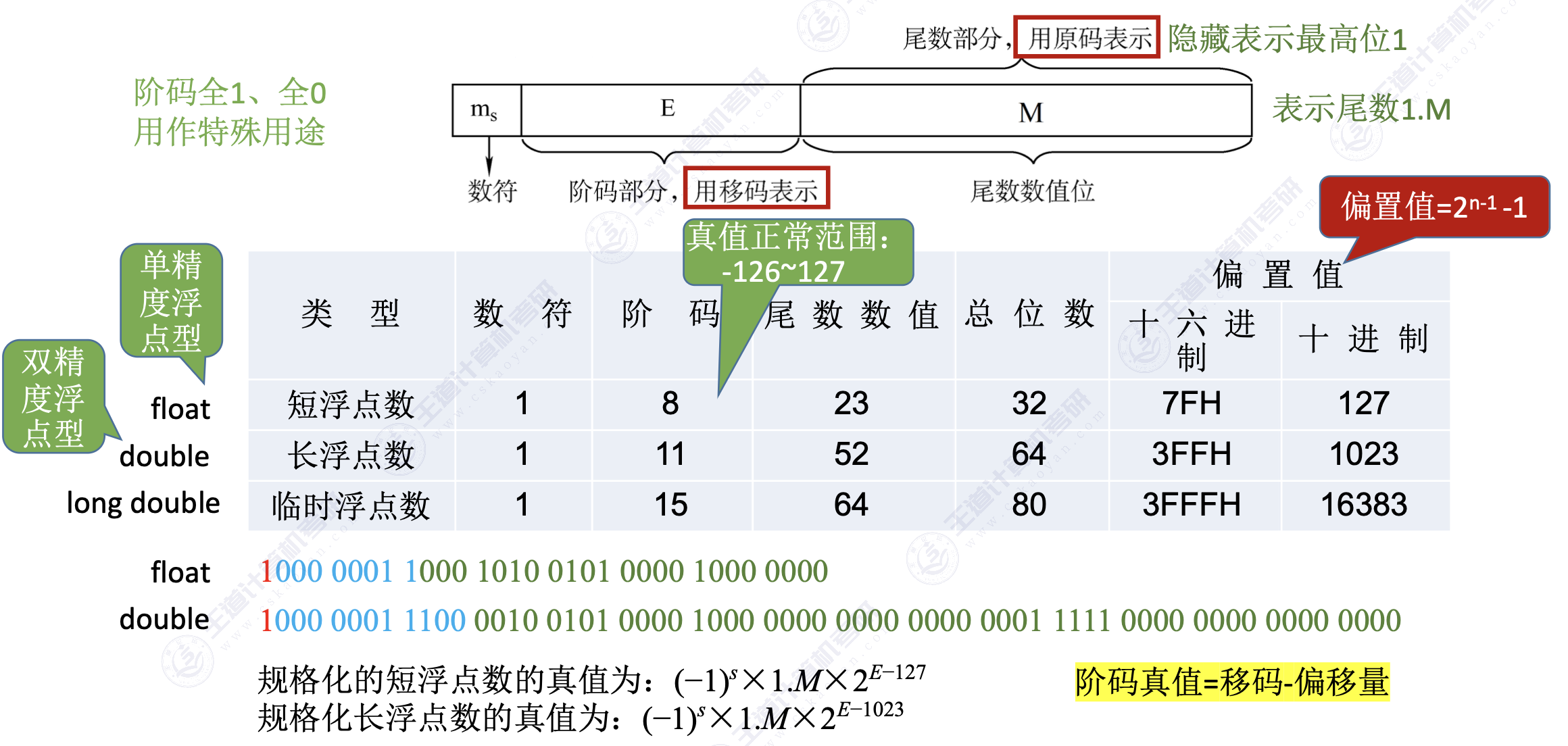
当阶码全为0或全为1 时:
阶码全为0,尾数=0时
- 符号为1:负零
- 符号为0:正零
阶码全为1,尾数=0时
- 符号为1:负无穷大
- 符号为0:正无穷大
阶码全为0,尾数不等0时
- 符号为1:非规格化负数
- 符号为0:非规格化正数
阶码全为1,尾数不等0时
- 符号0/1:无定义数(非数)
2.3.2 浮点数的加减运算
分以下几步:
1. 对阶
通过尾数移动,使得两个数的阶码相等
通常以小阶码向大阶码看齐,阶码小的尾数进行右移,阶码++,直至两个数的阶码相等
2. 尾数加减
尾数进行相加减
3. 尾数规格化
根据尾数的结果判断规格化使用右归or左归,参考2.3.1-3的规格化特点
4. 舍入
就近舍入
- “0舍1入”
- 若移除高位数值为0,则舍去
- 若移除的是1,则在末位加一
衡置一法
- 不管丢弃的是0还是1,末位衡置1
截断法
- 截取所需位数,丢弃后面的所有位
5. 溢出判断
在规格化和舍入是,可能结果会产生溢出
- 正指数超过了最大允许值,则发生指数上溢,产生异常
- 负指数超过了最小允许值,则发生指数下溢,结果按机器0处理
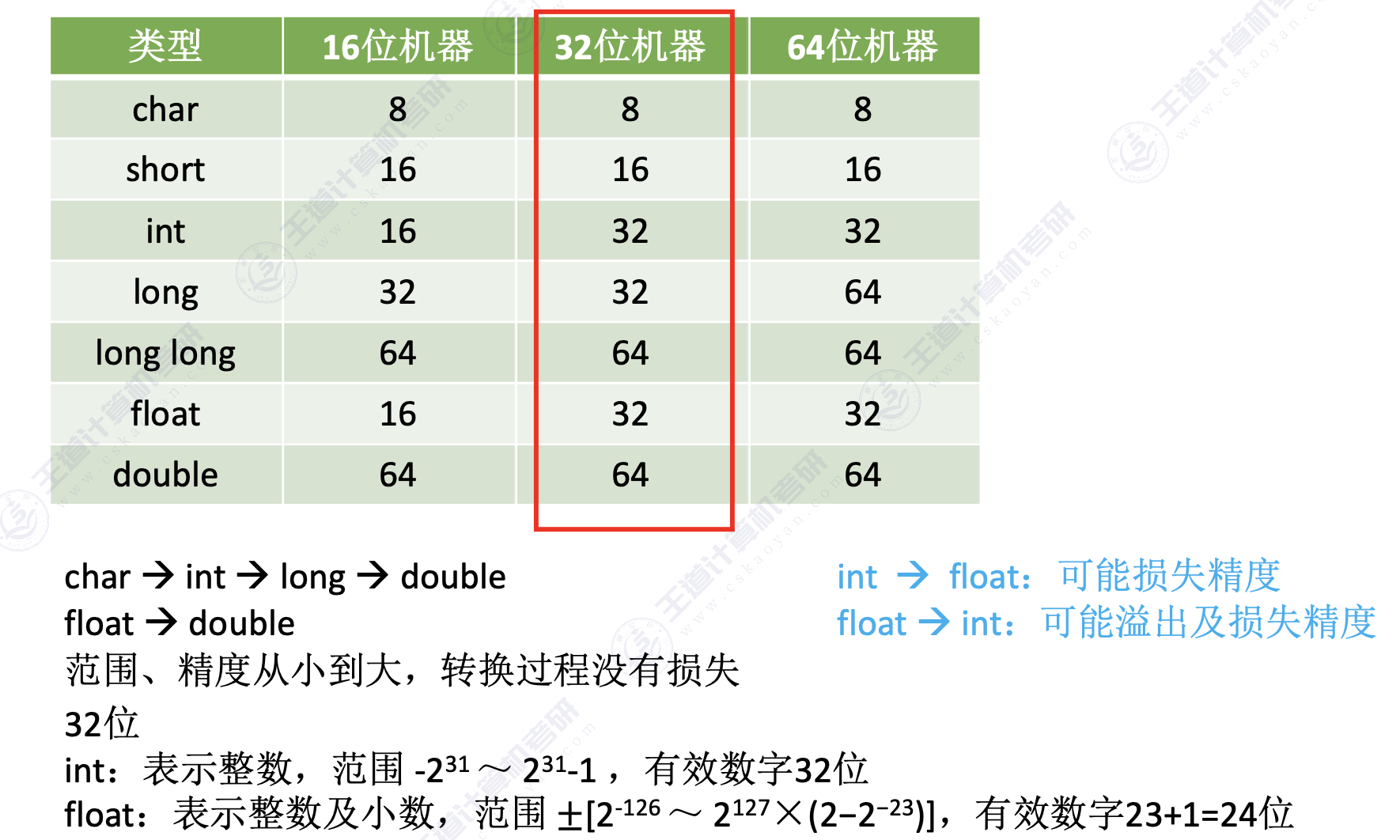
2.3.3 C语言中的浮点数类型
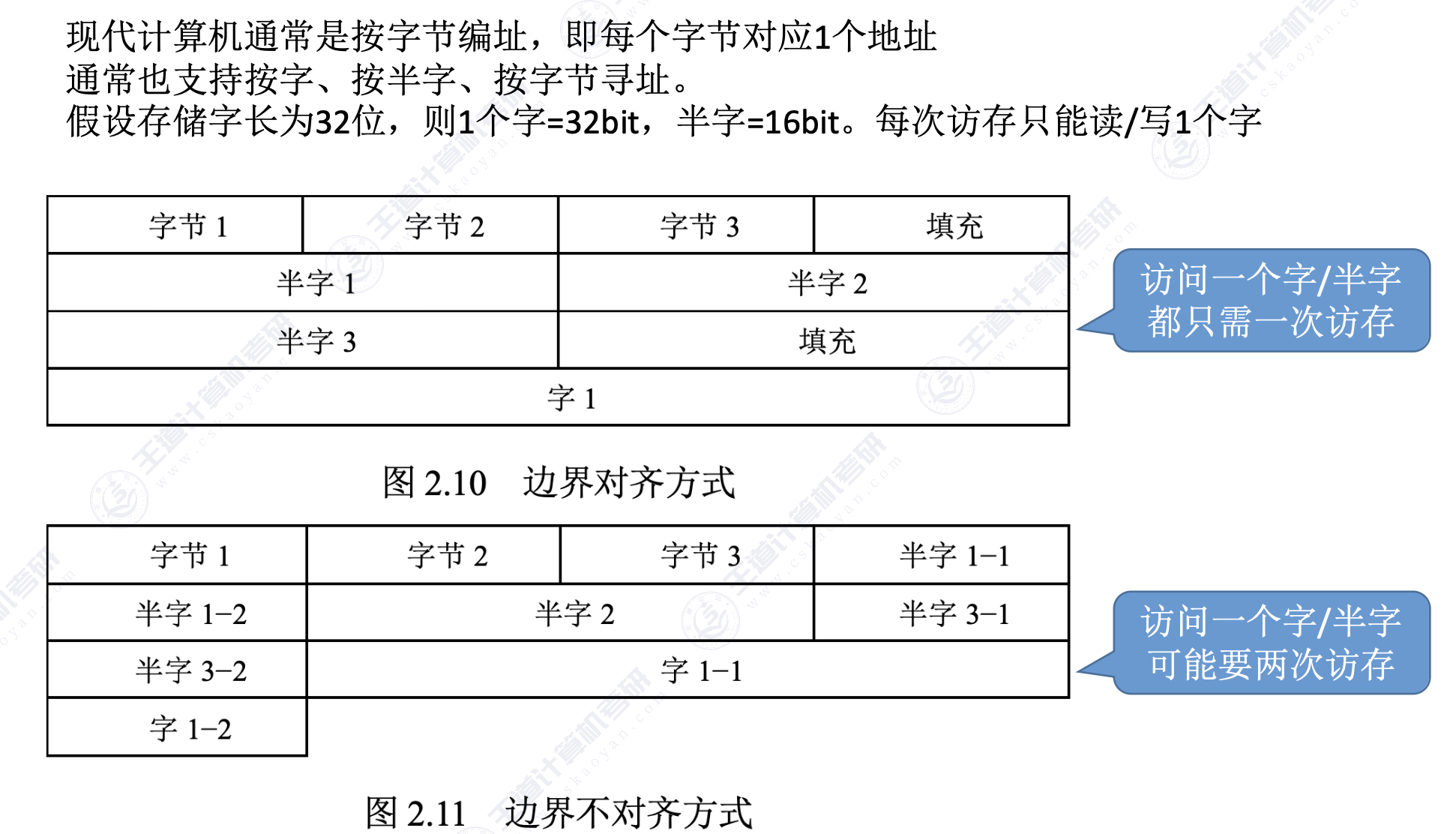
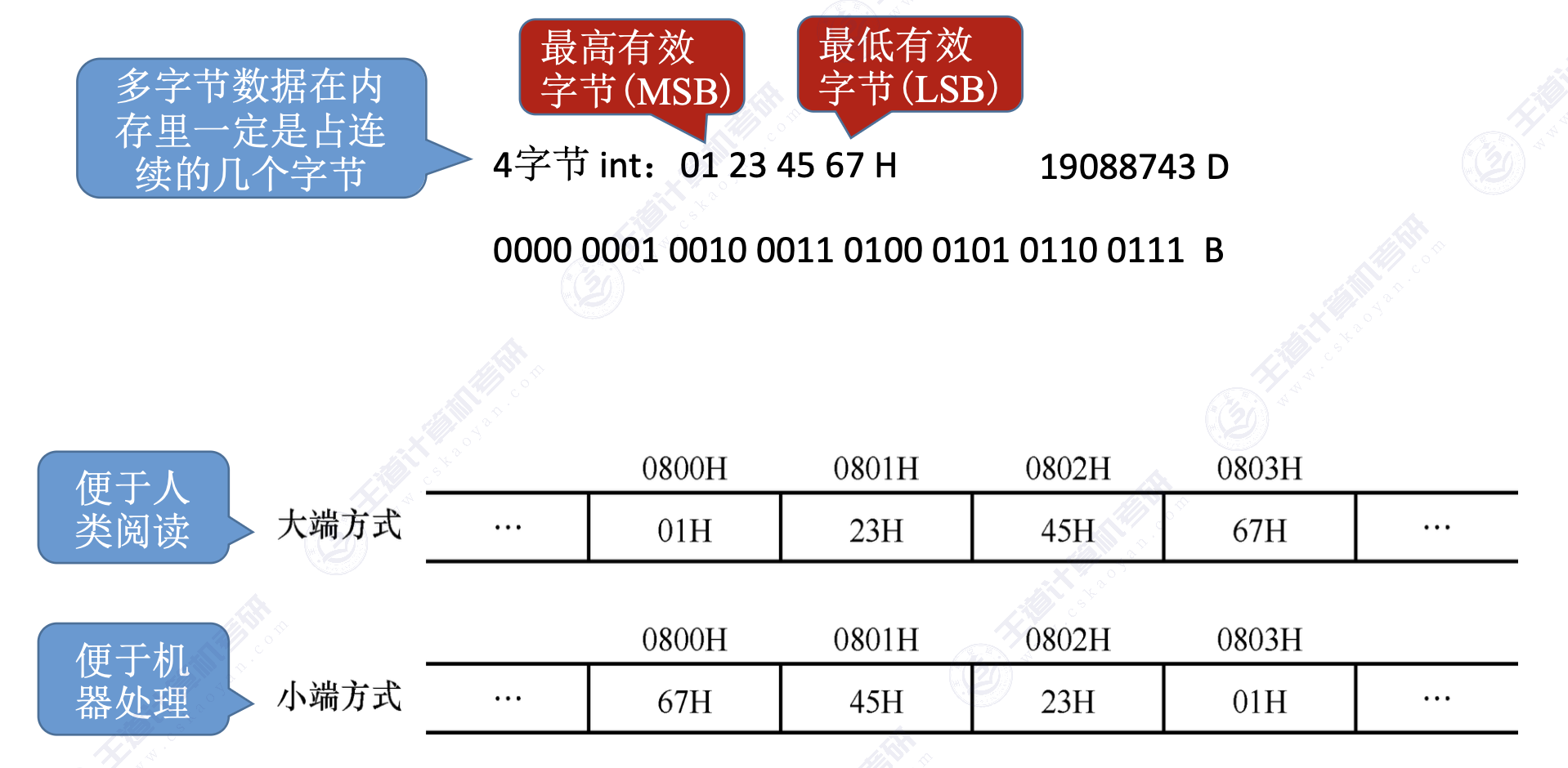
2.3.4 数据的大小端和对齐存储
1. 数据的“大端方式”和“小端方式”存储
2. 数据按“边界对齐”方式存储