《数据结构》第八章排序

Article

数据结构

8.1 排序的基本概念

8.1.1 排序的定义

排序（Sort），就是重新排列表中的元素，使表中的元素满⾜按关键字有序的过程。
算法的稳定性：若待排序表中有两个元素 $R_i$ 和 $R_j$，其对应的关键字相同即 $key_i = key_j$，且在排序前 $R_i$ 在 $R_j$ 的前⾯，若使⽤某⼀排序算法排序后，$R_i$ 仍然在$R_j$ 的前⾯，则称这个排序算法是稳定的，否则称排序算法是不稳定的。

排序算法分为两类：
- 内部排序
  数据都在内存中，关注如何使算法时、空复杂度更低。
- 外部排序
  数据太多，无法全部放入内存，还要关注如何使读/写磁盘次数更少。

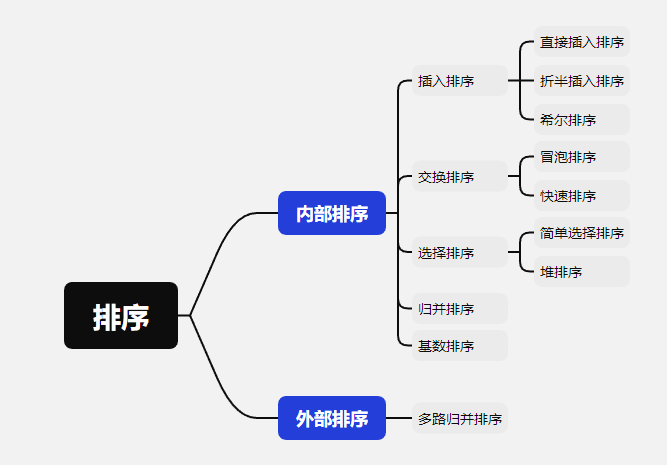
8.2 插入排序

8.2.1 直接插入排序

算法思想：每次将⼀个待排序的记录按其关键字⼤⼩插⼊到前⾯已排好序的⼦序列中，直到全部记录插⼊完成。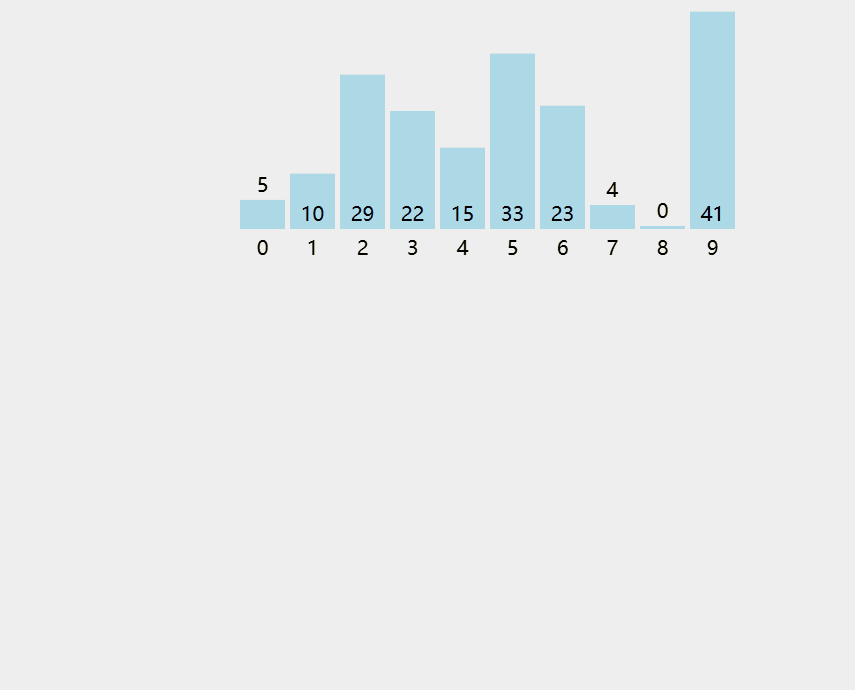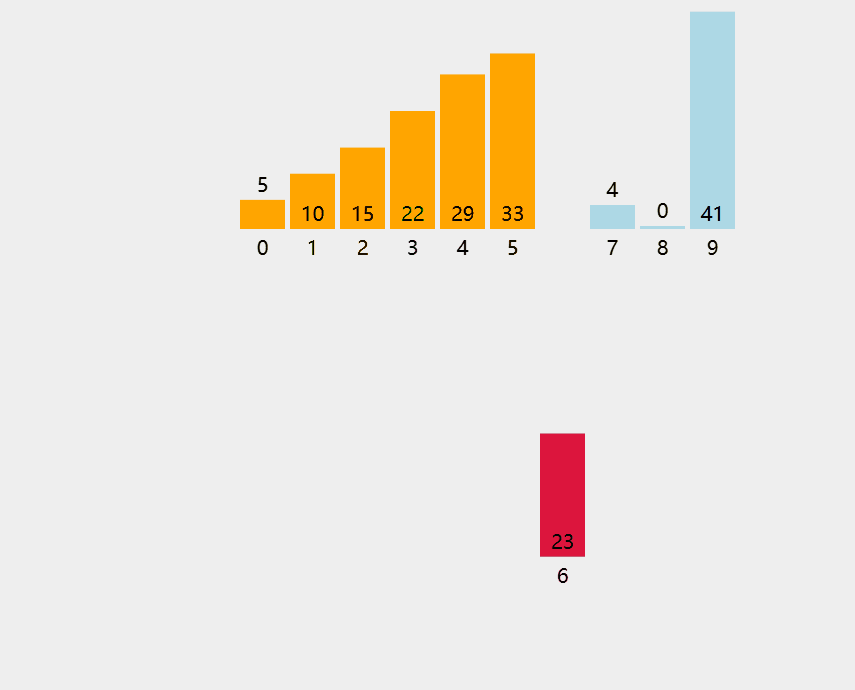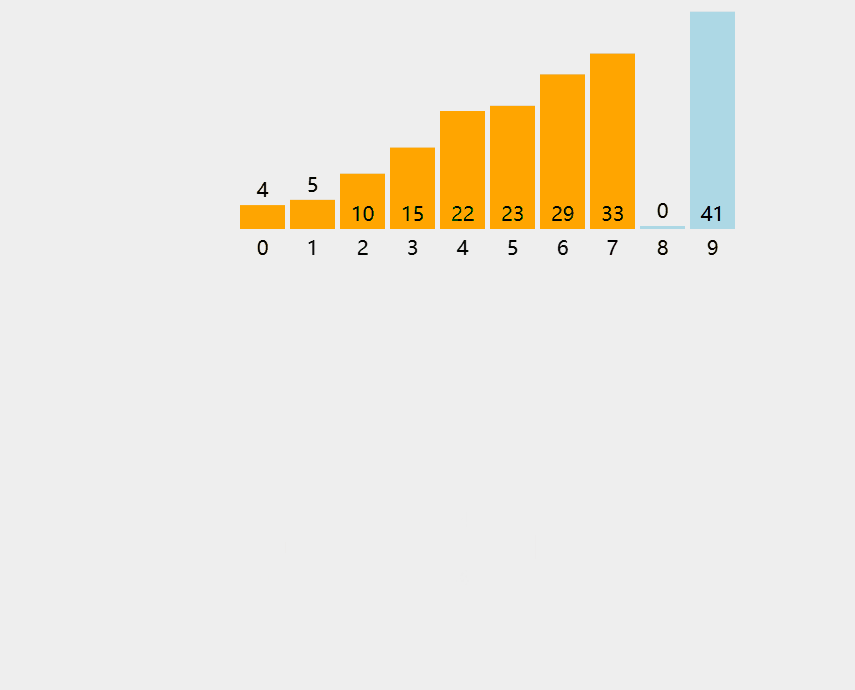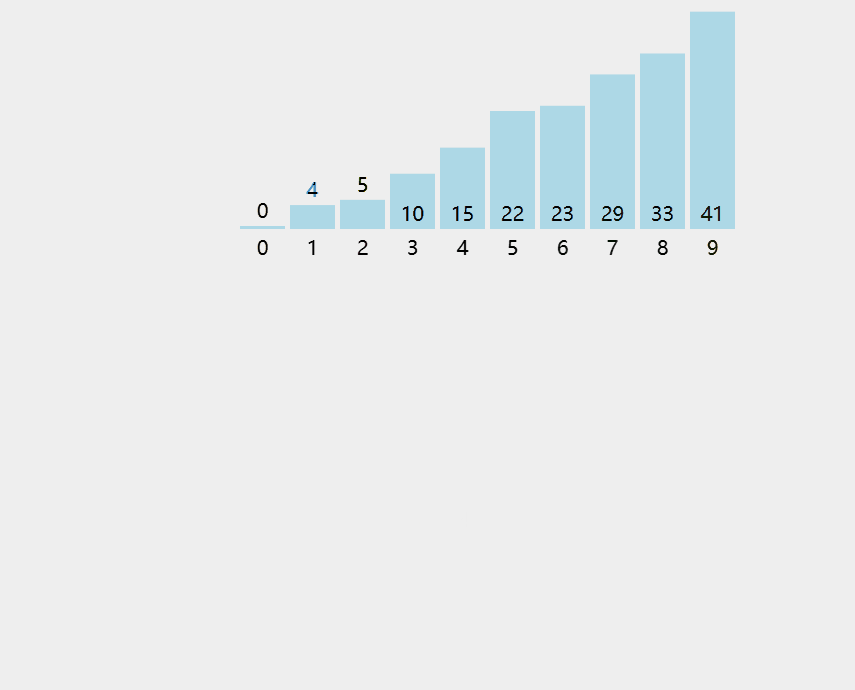

代码

♾️ C 代码:

void InsertSort (ElemType A[], int n){
  int i, j;
  for(i = 2; i<=n; i++){
      if(A[i] < A[i-1]){
          A[0] = A[i]; //哨兵
          for(j = i - 1; A[0]<A[j]; --j)
              A[j+1] = A[j];
          A[j+1] = A[0];
      }
  }
}

算法分析
- 空间复杂度： $O(1)$
- 时间复杂度：
  - 最好情况：原本有序，共 n-1 趟，每趟只需比较 1 次，不移动元素。 $O(n)$
  - 最坏情况：原本逆序，共 n-1 趟，第 n-1 趟需比较 n 次，移动元素 n+1 次。$O(n^2)$
  - 平均：$O(n^2)$
- 稳定性：稳定
- 适用性：顺序存储和链式存储。

8.2.2 折半插入排序

折半插入排序是在直接插入排序的基础上进行优化。在移动元素之前进行的查找阶段使用折半查找。

代码

♾️ C 代码:

void InsertSort(ElemType A[], int n){
  int i, j, low, high, mid;
  for(i = 2; i<=n; i++){
      if(A[i] < A[i-1]){
          A[0] = A[i-1];
          
          //查找方式与直接不同，使用折半查找
          low = 1; high = i-1;
          while(low <= high){
              mid = (low + high)/2;
              if(A[mid] > A[0])
                  high = mid - 1;
              else
                  low = mid + 1;
          }
          
          for(j = i - 1; j >= high + 1; --j)
              A[j+1] = A[j];
          A[high+1] = A[0];
      }
  }
}

算法分析
- 关键字比较减少，但移动次数依然没变，时间复杂度依然是 $O(n)$。
- 适用性：顺序存储。

8.2.3 希尔排序

算法思想：先将待排序表分割成若⼲形如 $L[i, i + d, i + 2d,…, i + kd]$ 的“特殊”⼦表，对各个⼦表分别进⾏直接插⼊排序。缩⼩增量 $d$ ，重复上述过程，直到 $d=1$ 为⽌。

代码

♾️ C 代码:

void ShellSort(ElemType A[], int n){
//A[0]只是暂存单元，不是哨兵，当 j<=0 时，插入位置已到
  int dk, i, j;
  for(dk = n/2; dk>=1; dk=dk/2){
      for(i = dk+1; i<=n; ++i){
          if(A[i]<A[i-dk]){
              A[0] = A[i];
              for(j=i-dk; j>0 && A[0]<A[j]; j-=dk)
                  A[j+dk] = A[j];
              A[j+dk] = A[0];
          }
      }
  }
}

算法分析
- 空间复杂度：$O(1)$
- 时间复杂度：最坏情况：$O(n^2)$
- 稳定性：不稳定
- 适用性：顺序存储。

8.3 交换排序

8.3.1 冒泡排序

算法思想：从后往前（或从前往后）两两⽐较相邻元素的值，若为逆序（即A[i-1]>A[i]），则交换它们，直到序列⽐较完。称这样过程为“⼀趟”冒泡排序。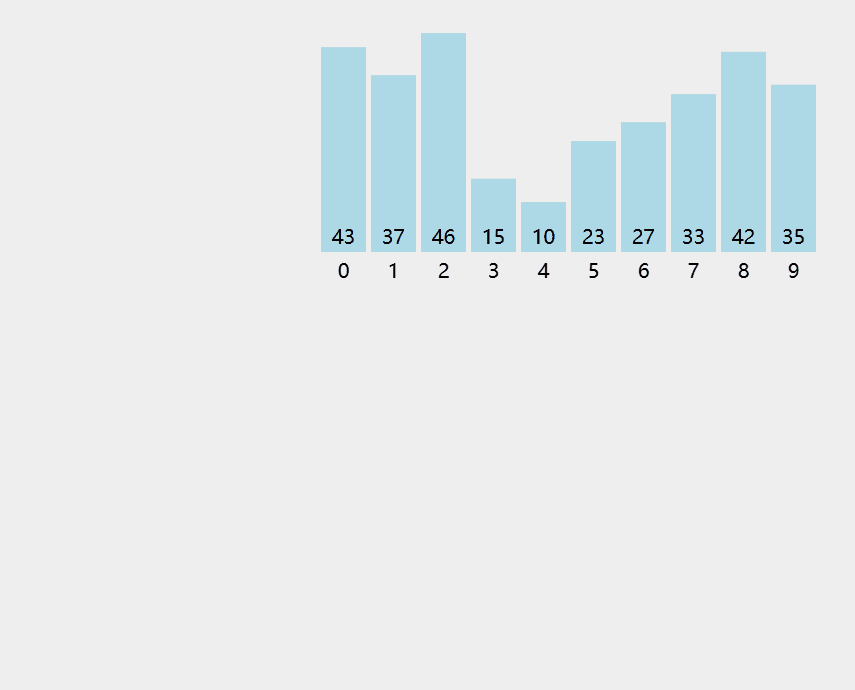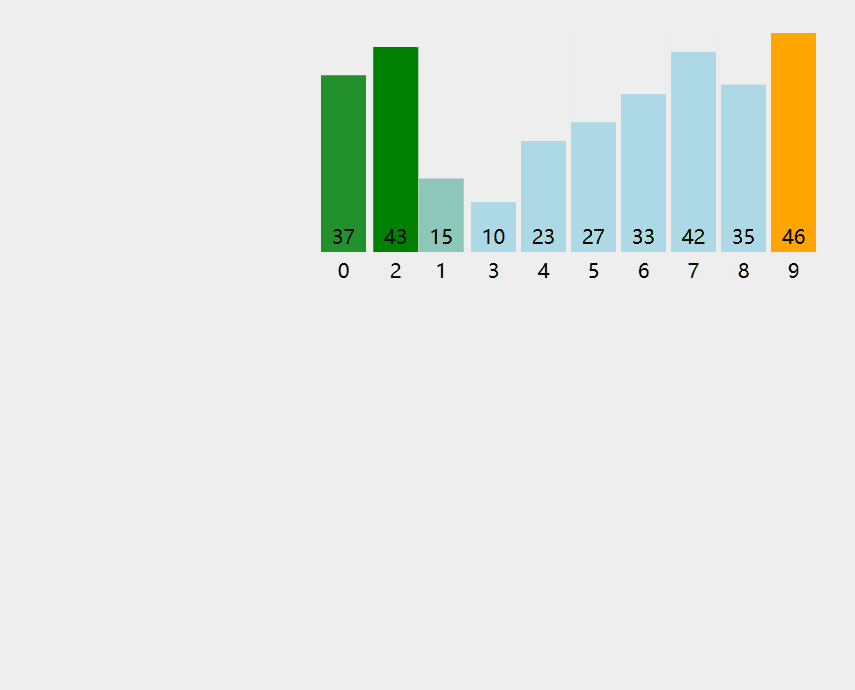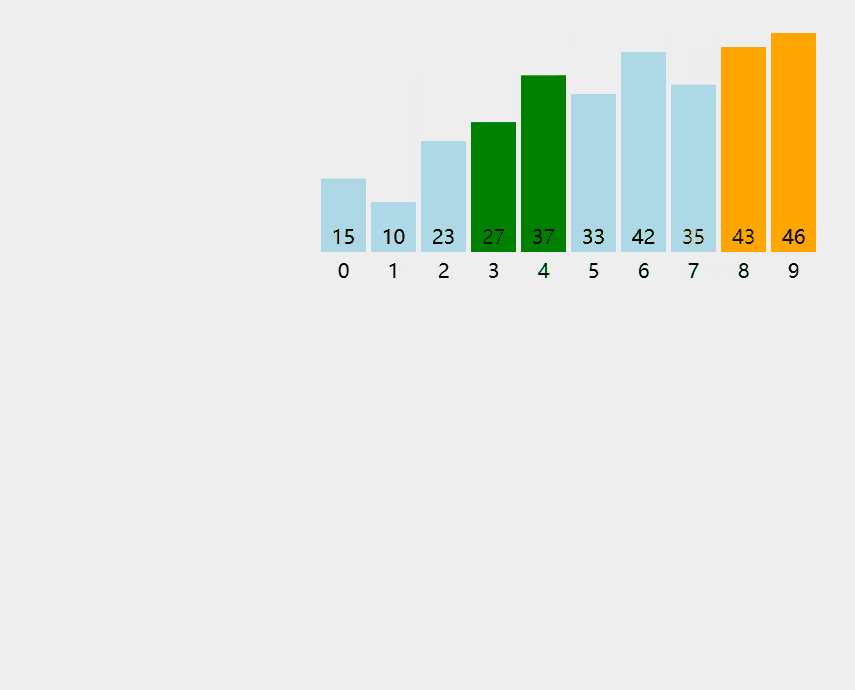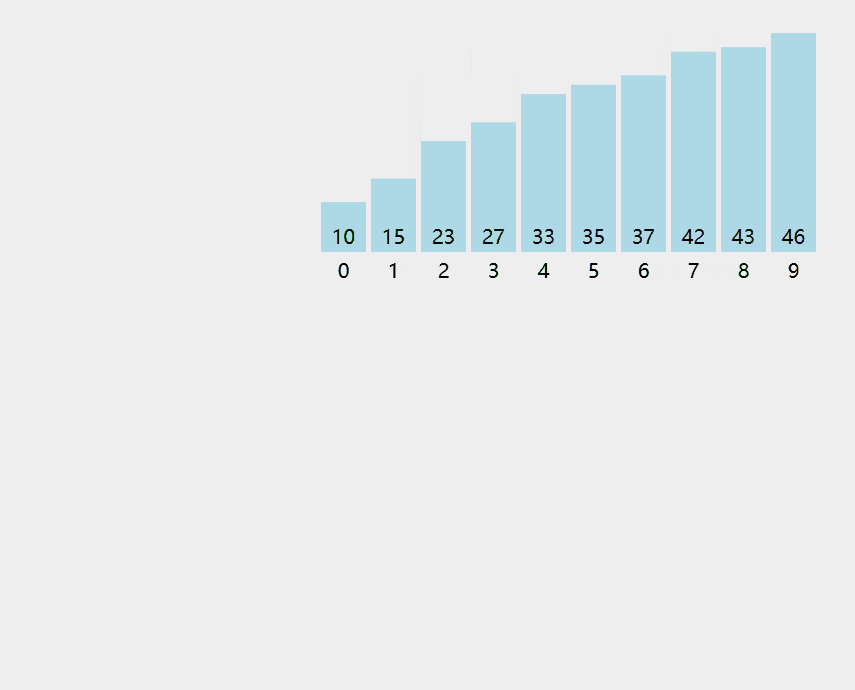

代码

♾️ C 代码:

void BubbleSort (ElemType A[], int n){
  for(int i=0; i<n-1; i++){
      bool flag = false;
      for(int j=n-1; j>i;j--){
          if(A[j-1]>A[j]){
              swap(A[j-1], A[j]); //封装好的swap交换函数
              flag = true;
          }
      }
      if(flag == false)
          return;
  }
}

算法分析
- 空间复杂度：$O(1)$
- 时间复杂度：
  - 最好情况：有序时，比较次数 n-1 ，交换次数 0。$O(n)$
  - 最坏情况：逆序时，比较次数=交换次数=$\frac{n(n-1)}{2}$，移动元素次数 $\frac{3n(n-1)}{2}$ （每交换一次，需要移动 3次元素，swap函数封装）。$O(n^2)$
  - 平均：$O(n^2)$
- 稳定性：不稳定
- 适用性：顺序存储和链式存储。

8.3.2 快速排序

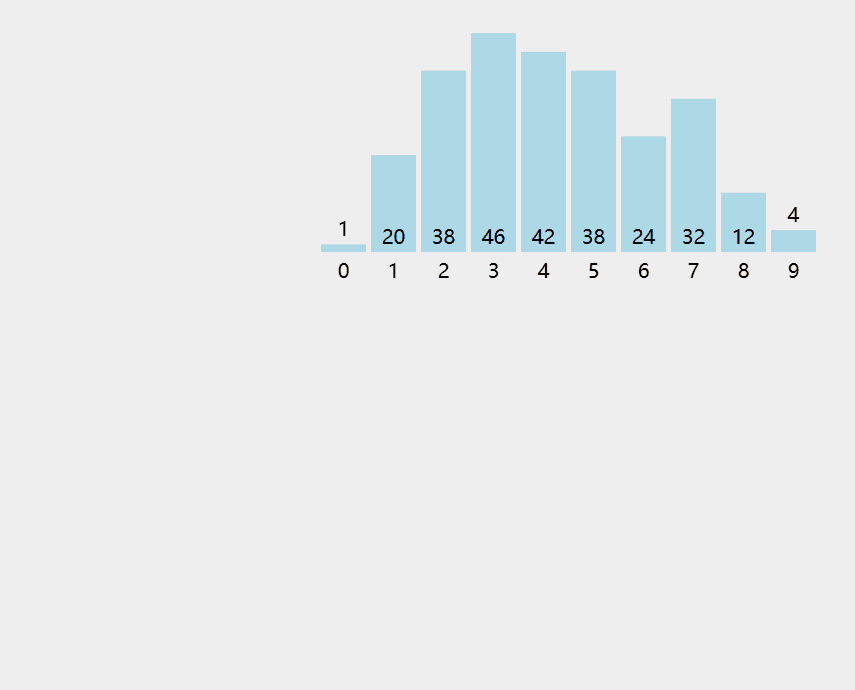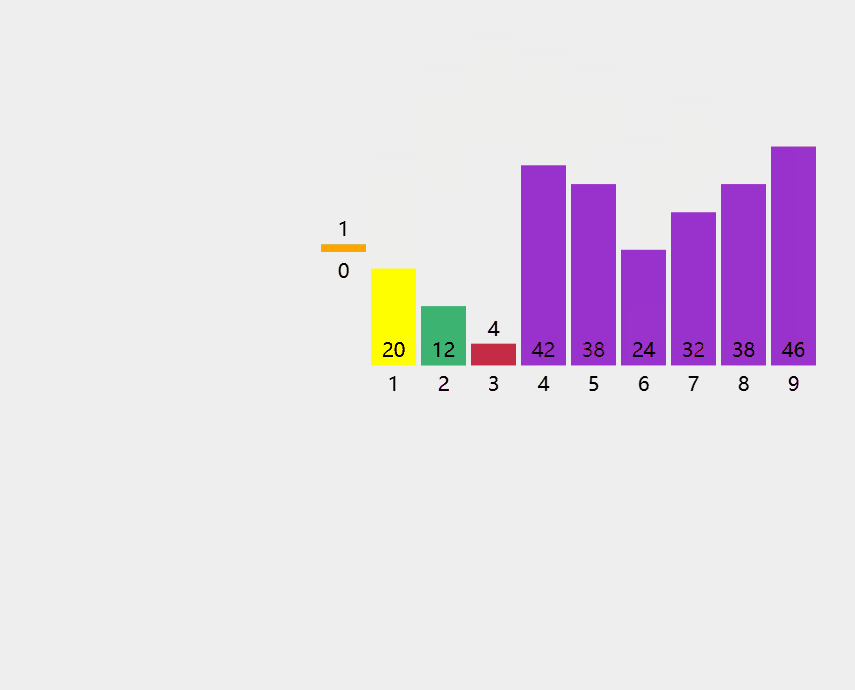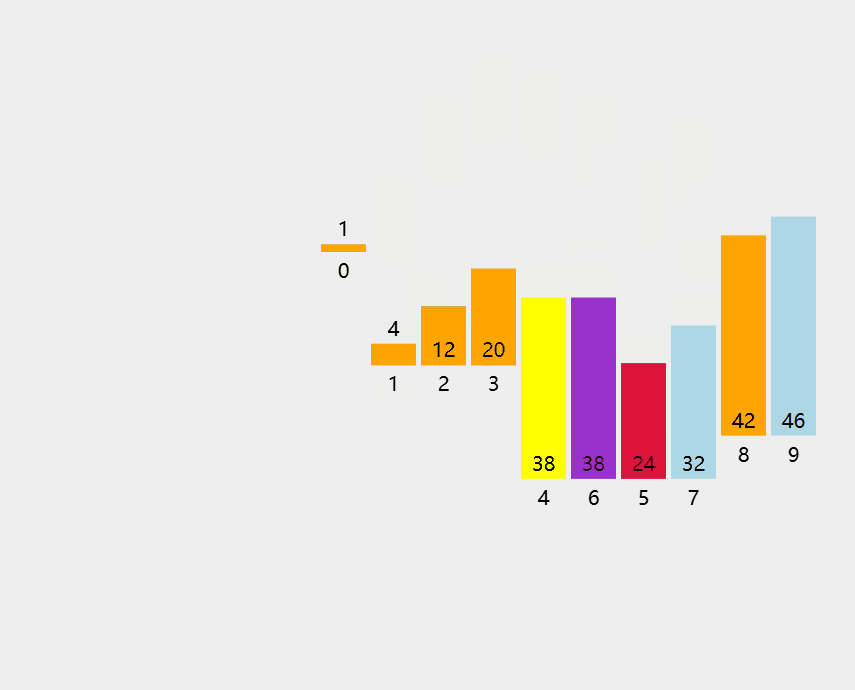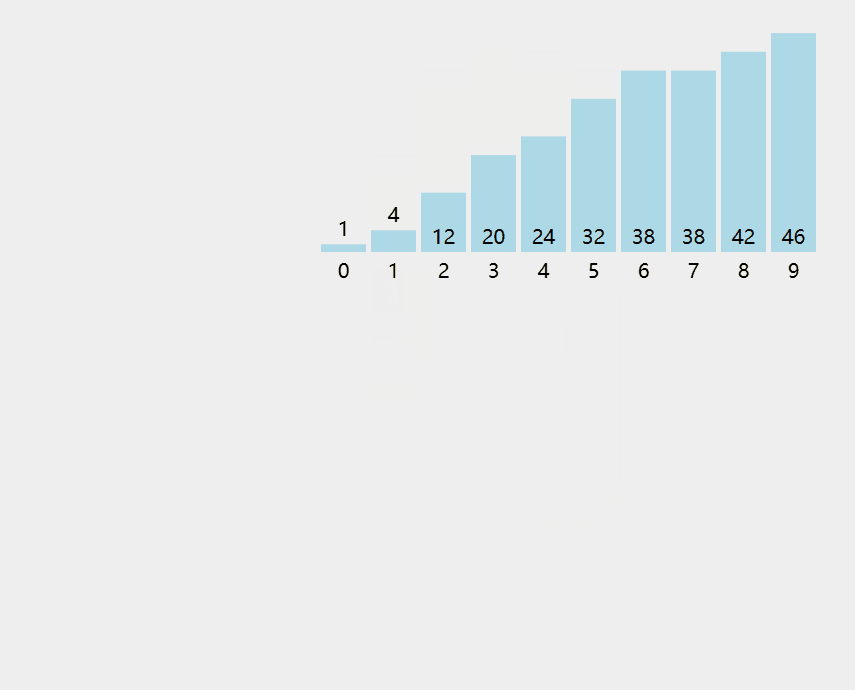
代码

♾️ C 代码:

void QuickSort(ElemType A[], int low, int high){
  if(low<high){
      int pivotpos = Partition(A, low, high);
      QuickSort(A, low, pivotpos-1);
      QuickSort(A, pivotpos+1, high);
  }
}

//划分函数
int Partition(ElemType A[], int low, int high){
  int pivot = A[low];
  while(low<high){
      while (low<high && A[high] >= pivot)
          --high;
      A[low] = A[high];
      while(low<high && A[low] <= pivot)
          ++low;
      A[high] = A[low];
  }
  A[low] = pivot;
  return low;
}

算法分析
- 空间复杂度：$O(递归层数)$，递归层数为其二叉树的层数。
- 时间复杂度=$O(n\times 递归层数)$
  - 最好情况：$O(n\log_{2}{n})$
  - 最坏情况：$O(n^2)$
  - 平均情况：$O(n\log_{2}{n})$
- 稳定性：不稳定
- 适用性：顺序存储。

快速排序是所有内部排序算法中平均性能最优的排序算法。

8.4 选择排序

8.4.1 简单选择排序

每⼀趟在待排序元素中选取关键字最⼩的元素加⼊有序⼦序列。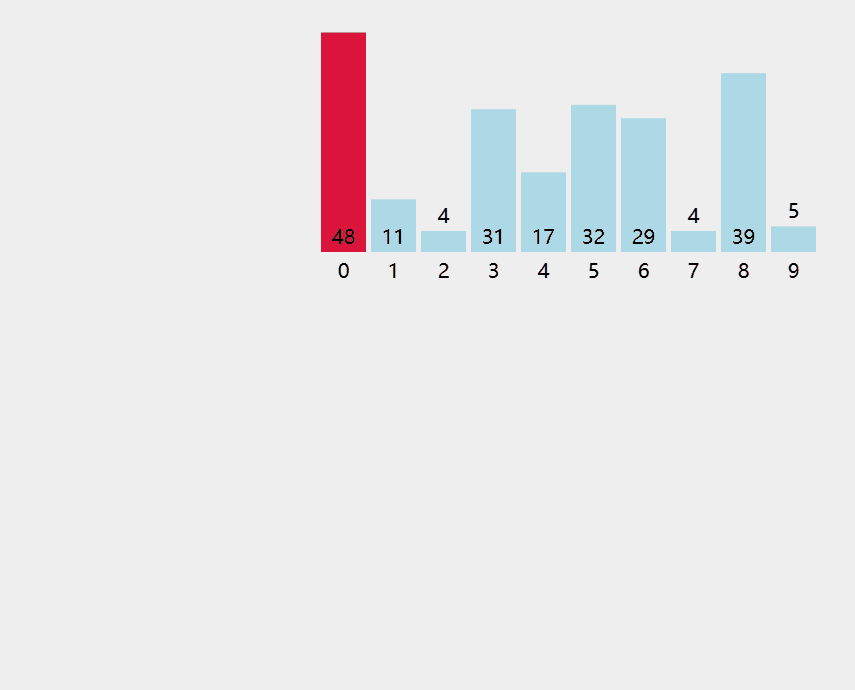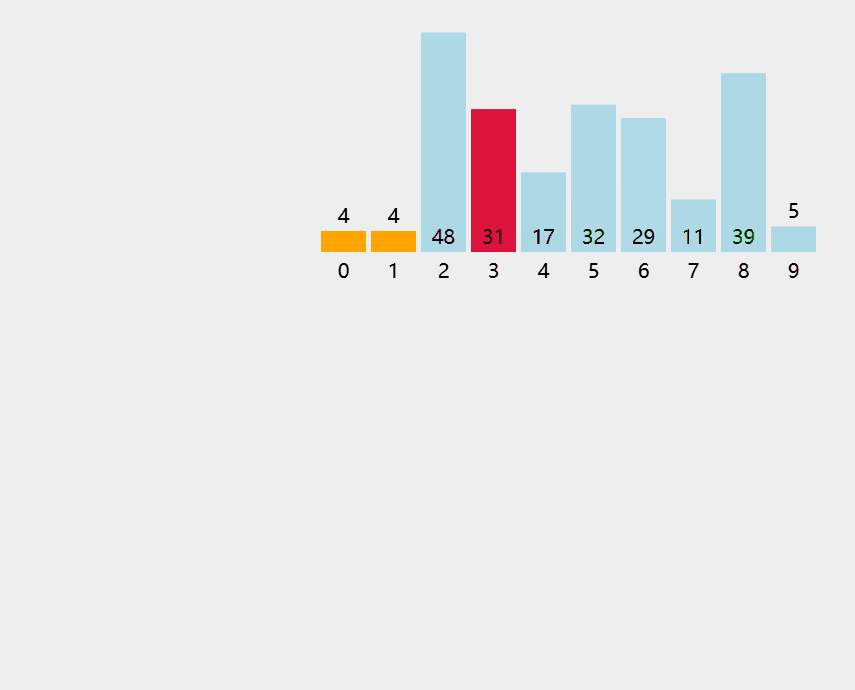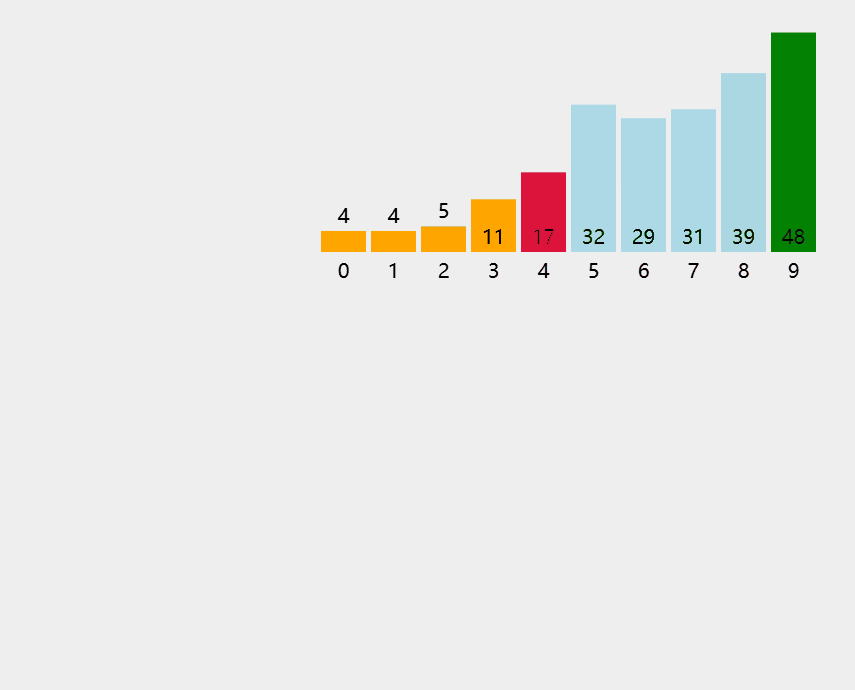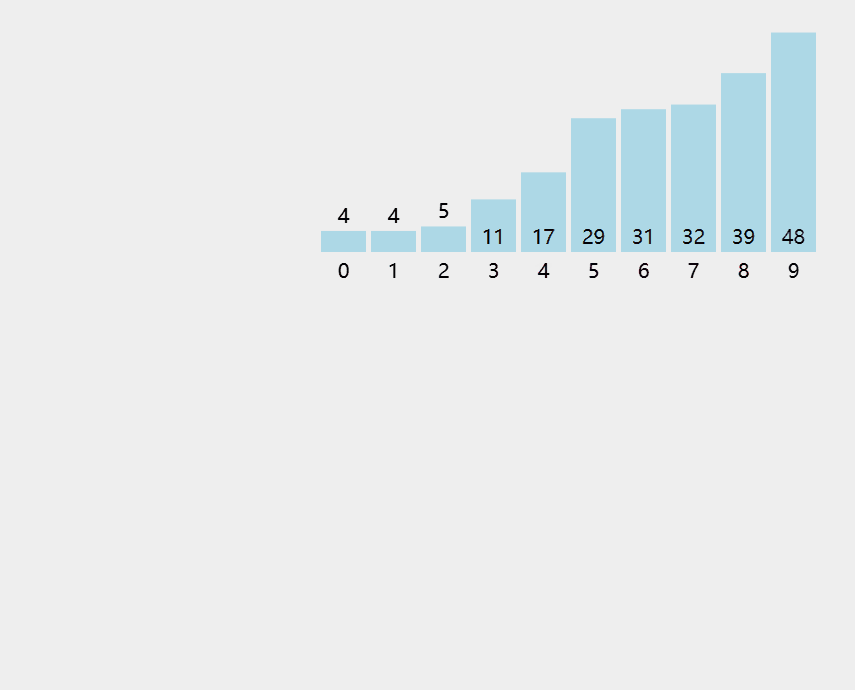

代码

♾️ C 代码:

void SelectSort(ElemType A[], int n){
  for(int i=0; i<n-1; i++){
      int min = i;
      for(int j=i+1; j<n; j++)
          if(A[j]<A[min])
              min = j;
      if(min != i)
          swap(A[i], A[min]);
  }
}

算法分析
- 空间复杂度：$O(1)$
- 时间复杂度：$O(n^2)$
- 稳定性：不稳定
- 适用性：顺序存储和链式存储

8.4.2 堆排序

代码

建立大根堆的算法

♾️ C 代码:

void BuildMaxHeap(ElemType A[], int len){
  for(int i=len/2; i>0; i--)
      HeadAdjust(A, i, len);
}

void HeadAdjust(ElemType A[], int k, int len){
  A[0] = A[k];
  for(int i=2*k; i<=lem; i*=2){
      if(i<len && A[i]<A[i+1])
          i++;
      if(A[0] >= A[i])
          break;
      else{
          A[k] = A[i];
          k = i;
      }
  }
  A[k] = A[0];
}

堆排序算法

♾️ C 代码:

void HeapSort(ElemType A[], int len){
  BuildMaxHeap(A, len);
  for(int i=len; i>1; i--){
      Swap(A[i], A[1]);
      HeadAdjust(A, 1, i-1);
  }
}

①大根堆->递增序列 ②小根堆->递减序列

算法分析
- 空间复杂度：$O(1)$
- 时间复杂度：$O(n\log_{2}{n})$
- 稳定性：不稳定
- 适用性：顺序存储

8.5 归并排序、基数排序和计数排序

8.5.1 归并排序

归并：把两个或多个已经有序的序列合并成⼀个。
可以把 m路归并操作视为一个倒置的 m叉树。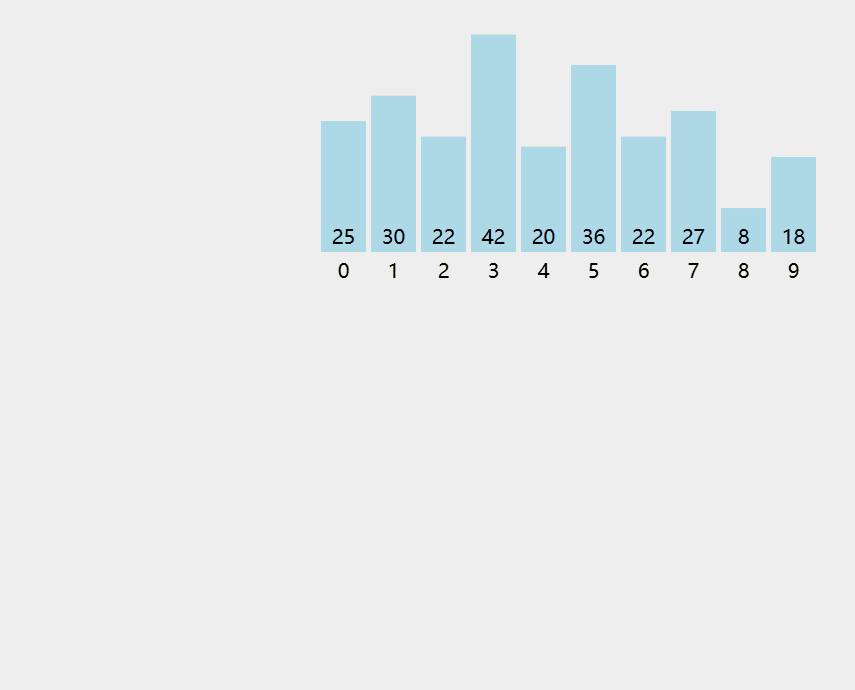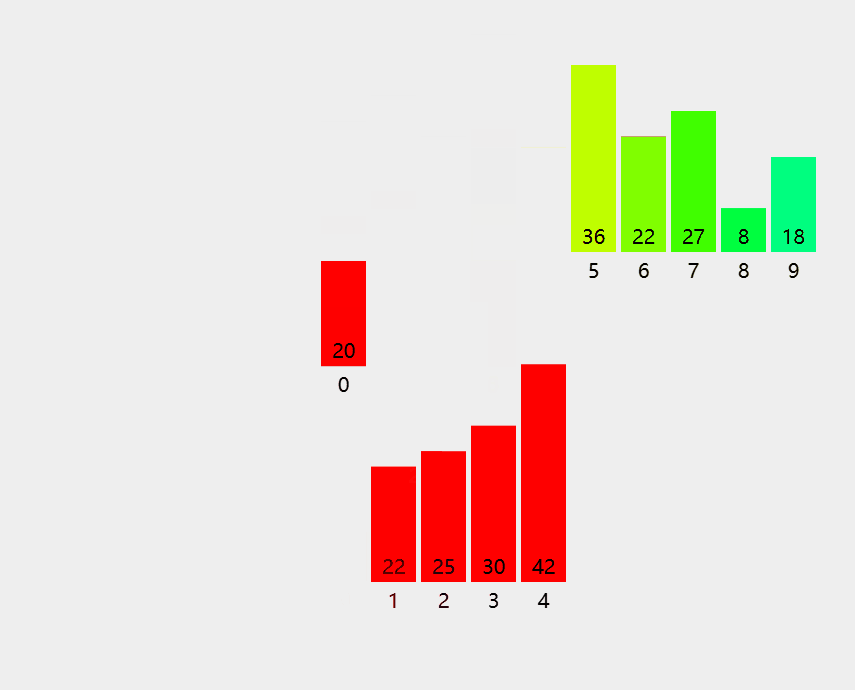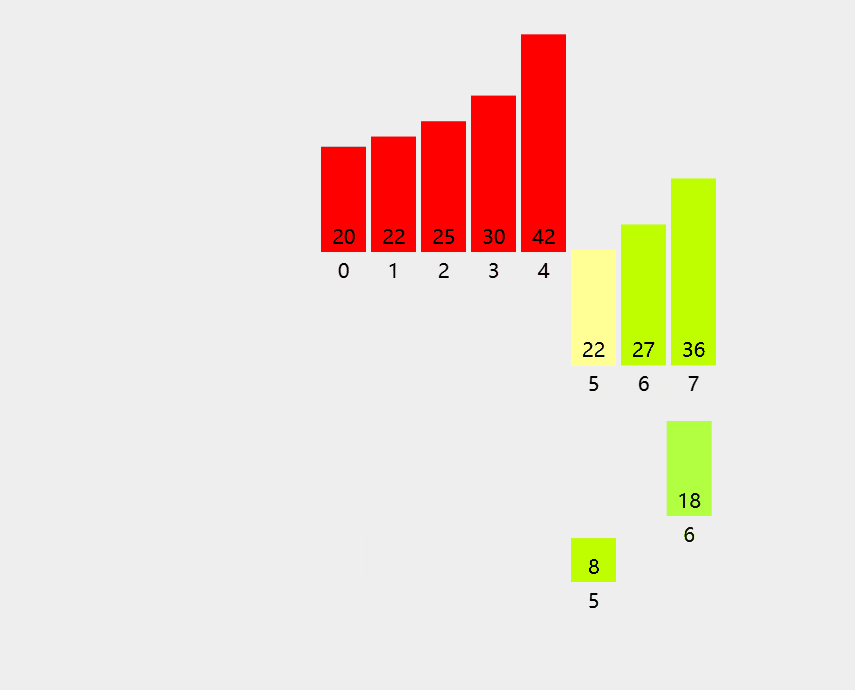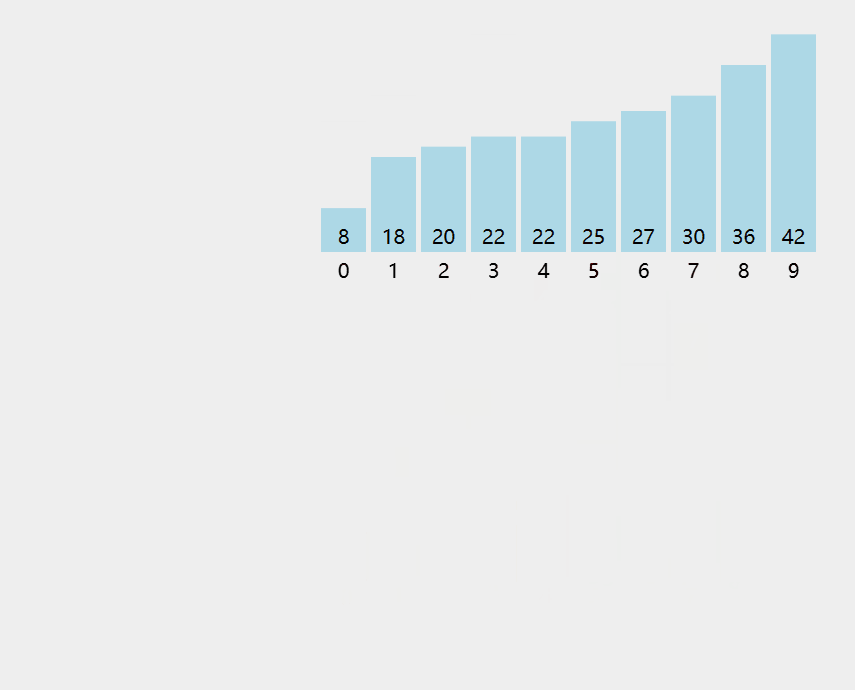

代码

归并函数

♾️ C 代码:

ElemType *B = (ElemType *)malloc((n+1)*sizeof(ElemType)); //辅助数组B
void Merge(ElemType A[], int low, int mid, int high){
  int i, j, k;
  for(k = low; k<=high; k++)
      B[k] = A[k]; //复制到B
  for(i = low, j=mid+1, k=i; i<=mid && j<=high; k++){
      if(B[i] <= B[j])
          A[k] = B[i++];
      else
          A[k] = B[j++];
  }
  while(i <= mid)
      A[k++] = B[i++];
  while(j <= high)
      A[k++] = B[j++];
}

归并排序算法

♾️ C 代码:

void MergeSort(ElemType A[], int low, int high){
  if(low<high){
      int mid = (low+high)/2;
      MergeSort(A, low, mid);
      MergeSort(A, mid+1, high);
      Merge(A, low, mid, high);
  }
}

算法分析
- 空间复杂度：主要受辅助数组 B 的影响。$O(n)$
- 时间复杂度：$O(n\log_{2}{n})$
- 稳定性：稳定
- 适用性：顺序存储和链式存储。

8.5.2 基数排序

算法分析
- 空间复杂度：需要 r 个辅助队列，$O(r)$
- 时间复杂度：$O(d(n+r))$
- 稳定性：稳定
- 适用性：顺序存储和链式存储。

8.6 各种内部排序算法的比较及应用

算法种类		时间复杂度			空间复杂度	适用性		是否稳定	xx是否与序列初始状态有关
		最好情况	平均情况	最坏情况		顺序存储	链式存储		趟数	比较次数
插入排序	直接插入排序	$O(n)$	$O(n^2)$	$O(n^2)$	$O(1)$	√	√	是	×	√
	希尔排序				$O(1)$	√	×	否	×	√
交换排序	冒泡排序	$O(n)$	$O(n^2)$	$O(n^2)$	$O(1)$	√	√	是	√	√
	快速排序	$O(n\log_{2}{n})$	$O(n\log_{2}{n})$	$O(n^2)$	$O(\log_{2}{n})$	√	×	否	√	√
选择排序	简单选择排序	$O(n^2)$	$O(n^2)$	$O(n^2)$	$O(1)$	√	√	否	×	×
	堆排序	$O(n\log_{2}{n})$	$O(n\log_{2}{n})$	$O(n\log_{2}{n})$	$O(1)$	√	×	否	×	√
其他	二路归并排序	$O(n\log_{2}{n})$	$O(n\log_{2}{n})$	$O(n\log_{2}{n})$	$O(n)$	√	√	是	×	√
	基数排序	$O(d(n+r))$	$O(d(n+r))$	$O(d(n+r))$	$O(r)$	√	√	是	×	×

8.7 外部排序

8.7.1 外部排序的基本概念

因处理数据太大，无法一次性读入内存，只能将数据一部分一部分调入内存进行排序，在排序过程需要多次进行内存和外存之间的交换。

8.7.2 外部排序的方法

在外部排序过程中的时间代价主要考虑访问磁盘的次数，即 I/O次数。
排序算法使用多路归并算法。

外部排序的总时间 = 内部排序的时间 + 外存信息 I/O 的时间 + 内部归并的时间

对于 k路归并，初始有 r个归并段，归并趟数 $S=\left \lceil \log_{k}{r} \right \rceil$。

8.7.3 多路平衡归并与败者树

1. 多路平衡归并

目的：增加归并路数 k
S趟归并总共需要的比较次数：

$$ S(n-1)(k-1)=\left \lceil \log_{k}{r} \right \rceil(n-1)(k-1)=\frac{\left \lceil \log_{2}{r} \right \rceil(n-1)(k-1)}{\left \lceil \log_{2}{k} \right \rceil} $$

2. 败者树

目的：减少比较次数。
S趟归并总共需要的比较次数：

$$ S(n-1)\left \lceil \log_{2}{k} \right \rceil=\left \lceil \log_{k}{r} \right \rceil(n-1)\left \lceil \log_{2}{k} \right \rceil=(n-1)\left \lceil \log_{2}{r} \right \rceil $$

8.7.4 置换-选择排序（生成初始归并段）

目的：减少归并段 r。

输出文件 FO	工作区 WA	输入文件 FI
-	-	17,21,05,44,10,12,56,32,29
-	17 21 05	44,10,12,56,32,29
05	17 21 44	10,12,56,32,29
05 17	21 44 10	12,56,32,29
05 17 21	44 10 12	56,32,29
05 17 21 44	10 12 56	32,29
05 17 21 44 56	10 12 32	29
05 17 21 44 56 #	10 12 32	29
10	12 32 29	-
10 12	32 29	-
10 12 29	32	-
10 12 29 32		-
10 12 29 32 #		-

8.7.5 最佳归并树

m路归并操作可以看作一个倒置的 m叉树。因此树的带权路径长度 WPL = 读次数 = 写次数。
所以 I/O次数 = 2 * WPL

当树为哈夫曼树时，其 WPL最小，所以读写次数最小。因此称该树为最佳归并树。

设度为 0 的结点有 $n_0$ 个，度为 k 的结点有 $n_k$ 个，归并树的结点总数为 $n$，则：

$n=n_k+n_0$ （总结点数 = 度为 k 的结点数 + 度为 0 的结点数）
$n=kn_k+1$ （总结点数 = 所有结点的度数之和 + 1）
因此得出 $n_k=\frac{n_0-1}{k-1}$
若 $(n_0-1) \%(k-1)=0$，能被整除，则正好可以构造 k 叉归并树。
若 $(n_0-1) \%(k-1)=u\ne 0$，不能被整除，则多余 u 个叶结点，因此需要增加 u 个值为 0 的内结点，去构造 k 叉归并树。

现在已有 66 次阅读，0 条评论，0 人点赞

日	一	二	三	四	五	六
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

《数据结构》第八章 排序

8.1 排序的基本概念

8.1.1 排序的定义

8.2 插入排序

8.2.1 直接插入排序

8.2.2 折半插入排序

8.2.3 希尔排序

8.3 交换排序

8.3.1 冒泡排序

8.3.2 快速排序

8.4 选择排序

8.4.1 简单选择排序

8.4.2 堆排序

8.5 归并排序、基数排序和计数排序

8.5.1 归并排序

8.5.2 基数排序

8.6 各种内部排序算法的比较及应用

8.7 外部排序

8.7.1 外部排序的基本概念

8.7.2 外部排序的方法

8.7.3 多路平衡归并与败者树

1. 多路平衡归并

2. 败者树

8.7.4 置换-选择排序（生成初始归并段）

8.7.5 最佳归并树

《数据结构》第八章排序